题目内容
14.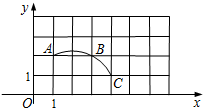 如图,在平面直角坐标系中,网格中小正方形的边长为1个单位长度,过格点A,B,C作一圆弧.
如图,在平面直角坐标系中,网格中小正方形的边长为1个单位长度,过格点A,B,C作一圆弧.(1)请写出该圆弧所在圆的圆心D的坐标(2,0);
(2)过点B画一条直线,使它与该圆弧相切(保留作图过程中的痕迹);
(3)若画出该圆弧所在圆,则在整个平面直角坐标系网格中共经过8个格点.
分析 (1)利用网格特点,画弦AB和BC的垂直平分线,根据垂径定理得到它们的交点坐标即为D点坐标;
(2)作直线BD,然后利用网格特点,过点B画该圆弧所在圆的圆心D的坐标直线EF垂直于BD即可;
(3)⊙D的半径为$\sqrt{5}$,在x轴上方可得到4个满足条件的格点,利用对称可得到在x轴下方有4个格点满足条件.
解答 解:(1)该圆弧所在圆的圆心D的坐标为(2,0);
(2)如图,EF为所作;
(3)⊙D经过的格点有((0,1),(0,-1),(1,2),(1,-2),(3,2),(3,-2),(4,1),(4,-1).
故答案为(2,0),8.
点评 本题考查了切线的判定定理:经过半径的外端且垂直于这条半径的直线是圆的切线.要证某线是圆的切线,已知此线过圆上某点,连接圆心与这点(即为半径),再证垂直即可.也考查了坐标与图形性质和垂径定理.

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案 小学课时特训系列答案
小学课时特训系列答案
相关题目
4.用配方法解方程x2+4x+1=0,则配方正确的是( )
| A. | (x+2)2=3 | B. | (x+2)2=-5 | C. | (x+2)2=-3 | D. | (x+4)2=3 |
2.亚奥理事会于2015年9月16日在土库曼斯坦阿什哈巴德举行第34届代表大会,并在会上投票选出2022年第19届亚运会举办城市为杭州.5个城市的国际标准时间(单位:时)在数轴上表示如图所示,那么北京时间2015年9月16日20时应是( )


| A. | 伦敦时间2015年9月16日11时 | B. | 巴黎时间2015年9月16日13时 | ||
| C. | 智利时间2015年9月16日5时 | D. | 曼谷时间2015年9月16日18时 |
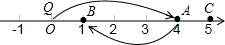 如图,数轴上一电子跳蚤Q从原点0出发,第1次沿数轴向右跳4个单位长度落在点A,第2次从点A出发沿数轴向左跳3个单位长度落在点B,第3次从点B沿数轴向右跳4个单位长度落在点C,第4次从点C出发沿数轴向左跳3个单位长度落在点D,…,按此规律继续跳动.
如图,数轴上一电子跳蚤Q从原点0出发,第1次沿数轴向右跳4个单位长度落在点A,第2次从点A出发沿数轴向左跳3个单位长度落在点B,第3次从点B沿数轴向右跳4个单位长度落在点C,第4次从点C出发沿数轴向左跳3个单位长度落在点D,…,按此规律继续跳动.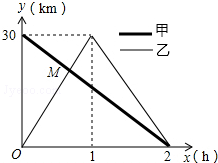 在一条笔直的公路上有A、B两地,甲乙两人同时出发,甲骑自行车从
在一条笔直的公路上有A、B两地,甲乙两人同时出发,甲骑自行车从