题目内容
3.计算:(1)-20+14-18+13
(2)(-$\frac{3}{4}$+$\frac{7}{12}-\frac{5}{9}$)$÷(-\frac{1}{36})$
(3)$\root{3}{-64}$+$\sqrt{\frac{16}{9}}$-|-3|
(4)-23×(-1$\frac{1}{2}$)2+5×(-6)-(-4)3÷8.
分析 (1)直接利用有理数加减运算法则化简求出即可;
(2)直接利用有理数除法运算法则化简求出即可;
(3)直接利用二次根式以及立方根的性质、绝对值的性质化简求出即可;
(4)直接利用乘方以及有理数乘除运算法则化简求出即可.
解答 解:(1)-20+14-18+13
=-6-18+13
=-24+13
=-11;
(2)(-$\frac{3}{4}$+$\frac{7}{12}-\frac{5}{9}$)$÷(-\frac{1}{36})$
=(-$\frac{3}{4}$+$\frac{7}{12}-\frac{5}{9}$)×(-36)
=27-21+20
=26;
(3)$\root{3}{-64}$+$\sqrt{\frac{16}{9}}$-|-3|
=-4+$\frac{4}{3}$-3
=-5$\frac{2}{3}$;
(4)-23×(-1$\frac{1}{2}$)2+5×(-6)-(-4)3÷8
=-8×$\frac{9}{4}$-30+64÷8
=-18-30+8
=-40.
点评 此题主要考查了实数运算,正确利用相关性质化简各数是解题关键.

练习册系列答案
相关题目
18.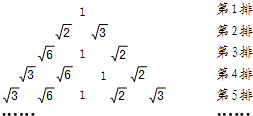 如图将1、$\sqrt{2}$、$\sqrt{3}$、$\sqrt{6}$按下列方式排列.若规定(m,n)表示第m排从左向右第n个数,则(5,4)与(15,8)表示的两数之积是( )
如图将1、$\sqrt{2}$、$\sqrt{3}$、$\sqrt{6}$按下列方式排列.若规定(m,n)表示第m排从左向右第n个数,则(5,4)与(15,8)表示的两数之积是( )
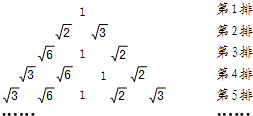 如图将1、$\sqrt{2}$、$\sqrt{3}$、$\sqrt{6}$按下列方式排列.若规定(m,n)表示第m排从左向右第n个数,则(5,4)与(15,8)表示的两数之积是( )
如图将1、$\sqrt{2}$、$\sqrt{3}$、$\sqrt{6}$按下列方式排列.若规定(m,n)表示第m排从左向右第n个数,则(5,4)与(15,8)表示的两数之积是( )| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{6}$ | D. | 3$\sqrt{2}$ |
8.已知命题“若a=b,则a2=b2”,则该命题的逆命题为( )
| A. | 若a≠b,则a2=b2 | B. | 若a2=b2,则a≠b | C. | 若a=b,则a2≠b2 | D. | 若a2=b2,则a=b |
15.下列实数中,属于无理数的是( )
| A. | $\frac{2}{3}$ | B. | $\sqrt{3}$ | C. | -5 | D. | 0 |
12.下列各数中是无理数的是( )
| A. | $\sqrt{2}$ | B. | 3.14 | C. | $\root{3}{8}$ | D. | $\frac{1}{3}$ |
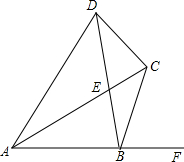 已知:AB=2,AC平分∠DAB,∠DAB+∠DCB=180°,∠DCB=120°,当∠ABD=∠CBF时,则AC=$\sqrt{3}$+1.
已知:AB=2,AC平分∠DAB,∠DAB+∠DCB=180°,∠DCB=120°,当∠ABD=∠CBF时,则AC=$\sqrt{3}$+1.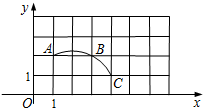 如图,在平面直角坐标系中,网格中小正方形的边长为1个单位长度,过格点A,B,C作一圆弧.
如图,在平面直角坐标系中,网格中小正方形的边长为1个单位长度,过格点A,B,C作一圆弧. 如图,四边形ABCD的对角线AC与BD相交于O点,∠1=∠2,∠3=∠4.
如图,四边形ABCD的对角线AC与BD相交于O点,∠1=∠2,∠3=∠4.