题目内容
4. 在一条笔直的公路上有A、B两地,甲乙两人同时出发,甲骑自行车从
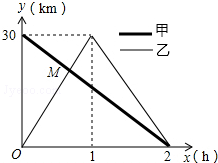
在一条笔直的公路上有A、B两地,甲乙两人同时出发,甲骑自行车从A地到B地;乙骑自行车从B地到A地,到达A地后立即按原路返回,如
图是甲、乙两人离B地的距离y(km)与行驶时间x(h)之间的函数图象,根据图象解答以下问题:
(1)写出A、B两地的距离;
(2)求出点M的坐标,并解释该点坐标所表示的意义.
分析 (1)当x=0时,甲的y值即为A、B两地的距离;
(2)根据图象求出甲、乙两人的速度,再利用相遇问题求出相遇时间,然后求出乙的路程即可得到点M的坐标以及实际意义.
解答 解:(1)x=0时,甲距离B地30千米,
所以,A、B两地的距离为30千米;
(2)由图可知,甲的速度:30÷2=15千米/时,
乙的速度:30÷1=30千米/时,
30÷(15+30)=$\frac{2}{3}$,
$\frac{2}{3}$×30=20千米,
所以,点M的坐标为($\frac{2}{3}$,20),表示$\frac{2}{3}$小时后两车相遇,此时距离B地20千米.
点评 本题考查了一次函数的应用,正确理解函数图象横纵坐标表示的意义,理解问题的过程,就能够通过图象得到函数问题的相应解决.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
15.下列实数中,属于无理数的是( )
| A. | $\frac{2}{3}$ | B. | $\sqrt{3}$ | C. | -5 | D. | 0 |
12.下列各数中是无理数的是( )
| A. | $\sqrt{2}$ | B. | 3.14 | C. | $\root{3}{8}$ | D. | $\frac{1}{3}$ |
9.若关于x的方程(a-1)x2+2x-1=0是一元二次方程,则a的取值范围是( )
| A. | a≠1 | B. | a>1 | C. | a<1 | D. | a≠0 |
16.将抛物线y=2x2-1,先向上平移2个单位,再向右平移1个单位后其顶点坐标是( )
| A. | (2,1) | B. | (1,2) | C. | (1,-1) | D. | (1,1) |
14.已知关于x的一元二次方程x2+x+m2-4=0的一个根是0,则m的值是( )
| A. | 0 | B. | 1 | C. | 2 | D. | 2或-2 |
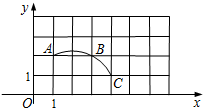 如图,在平面直角坐标系中,网格中小正方形的边长为1个单位长度,过格点A,B,C作一圆弧.
如图,在平面直角坐标系中,网格中小正方形的边长为1个单位长度,过格点A,B,C作一圆弧.