题目内容
已知四边形ABCD,对角线AC,BD交于点O.现给出四个条件:
①AC⊥BD;②AC平分对角线BD;③AD∥BC;④∠OAD=∠ODA.请你以其中的三个条件作为命题的题设,以“四边形ABCD为矩形”作为命题的结论.
(1)写出一个真命题,并证明;
(2)写出一个假命题,并举出一个反例说明.
①AC⊥BD;②AC平分对角线BD;③AD∥BC;④∠OAD=∠ODA.请你以其中的三个条件作为命题的题设,以“四边形ABCD为矩形”作为命题的结论.
(1)写出一个真命题,并证明;
(2)写出一个假命题,并举出一个反例说明.
考点:命题与定理
专题:证明题
分析:(1)以②③④为题设,以“四边形ABCD为矩形”为结论可组成一个真命题,根据对角线相等且互相平分的四边形为矩形进行证明;
(2)①②④为题设,以“四边形ABCD为矩形”为结论可组成一个假命题,然后利用画反例图进行说明.
(2)①②④为题设,以“四边形ABCD为矩形”为结论可组成一个假命题,然后利用画反例图进行说明.
解答:解:(1)真命题:四边形ABCD,对角线AC,BD交于点O,若AC平分对角线BD;AD∥BC;∠OAD=∠ODA,则四边形ABCD为矩形.
证明如下:如图, ∵∠OAD=∠ODA,
∵∠OAD=∠ODA,
∴OA=OD,
∵AD∥BC,
∴∠OAD=∠OCB,∠OBC=∠ODA,
∴∠OCB=∠OBC,
∴OB=OC,
∵AC平分对角线BD,
∴OB=OD,
∴OA=OB=OC=OD,
即对角线AC和BD相等且互相平分,
∴四边形ABCD为矩形;
(2)假命题:四边形ABCD,对角线AC,BD交于点O,若AC⊥BD,AC平分对角线BD;∠OAD=∠ODA,则四边形ABCD为矩形.
如图,
 .
.
证明如下:如图,
 ∵∠OAD=∠ODA,
∵∠OAD=∠ODA,∴OA=OD,
∵AD∥BC,
∴∠OAD=∠OCB,∠OBC=∠ODA,
∴∠OCB=∠OBC,
∴OB=OC,
∵AC平分对角线BD,
∴OB=OD,
∴OA=OB=OC=OD,
即对角线AC和BD相等且互相平分,
∴四边形ABCD为矩形;
(2)假命题:四边形ABCD,对角线AC,BD交于点O,若AC⊥BD,AC平分对角线BD;∠OAD=∠ODA,则四边形ABCD为矩形.
如图,
 .
.点评:本题考查了命题与定理:判断一件事情的语句,叫做命题.许多命题都是由题设和结论两部分组成,题设是已知事项,结论是由已知事项推出的事项,一个命题可以写成“如果…那么…”形式.有些命题的正确性是用推理证实的,这样的真命题叫做定理.也考查了矩形的判定.

练习册系列答案
相关题目
若一元二次方程(1-k)x2+2x-3=0有实数根,那么k的最大整数值是( )
| A、1 | B、2 | C、-1 | D、0 |
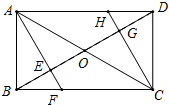 如图所示,矩形ABCD中,O是两条对角线的交点,AF垂直平分OB,垂足为E,CH垂直平分OD,垂足为G,求证:四边形AFCH是菱形.
如图所示,矩形ABCD中,O是两条对角线的交点,AF垂直平分OB,垂足为E,CH垂直平分OD,垂足为G,求证:四边形AFCH是菱形. 如图,已知∠BAC=∠DAE,AB=AD,要使△ABC≌△ADE,还需要添加的条件可以是
如图,已知∠BAC=∠DAE,AB=AD,要使△ABC≌△ADE,还需要添加的条件可以是 如图,已知AB∥ED,∠CAB=135°,∠ACD=80°,求∠CDE的度数.
如图,已知AB∥ED,∠CAB=135°,∠ACD=80°,求∠CDE的度数.