题目内容
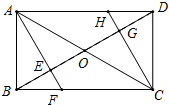 如图所示,矩形ABCD中,O是两条对角线的交点,AF垂直平分OB,垂足为E,CH垂直平分OD,垂足为G,求证:四边形AFCH是菱形.
如图所示,矩形ABCD中,O是两条对角线的交点,AF垂直平分OB,垂足为E,CH垂直平分OD,垂足为G,求证:四边形AFCH是菱形.考点:菱形的判定
专题:证明题
分析:根据矩形的性质推出OA=OB,根据线段垂直平分线的性质得出AB=OA,得出等边△OAB;根据矩形的性质得出AH∥CF,根据垂直得出AF∥CH,求出∠DAC=∠ACG=30°,推出AH=CH,根据平行四边形的判定和菱形的判定得出即可.
解答:证明:∵四边形ABCD是矩形,
∴OA=OC,OB=OD,AC=BD,
∴OA=OB=OC=OD,
∵AF垂直平分线段OB,
∴AB=OA,
∴AB=OA=OB,
∴△AOB是等边三角形,
∴AE⊥BD,
∴∠BAE=∠CAE=30°,
∵四边形ABCD是矩形,
∴AD∥BC,∠DAB=90°,
∴∠DAC=90°-30°-30°=30°,
∵四边形ABCD是矩形,
∴OA=OC,OB=OD,AC=BD,
∴OA=OB=OC=OD,
∵CH垂直平分线段OD,
∴CD=OC,
∴CD=OD=OC,
∴△DOC是等边三角形,
∵CG⊥BD,
∴∠DCG=∠ACG=30°,
∴∠DAC=∠ACG,
∴AH=CH,
∵AE⊥BD,CG⊥BD,
∴AF∥CH,
∵AD∥BC,
∴四边形AFCH是菱形.
∴OA=OC,OB=OD,AC=BD,
∴OA=OB=OC=OD,
∵AF垂直平分线段OB,
∴AB=OA,
∴AB=OA=OB,
∴△AOB是等边三角形,
∴AE⊥BD,
∴∠BAE=∠CAE=30°,
∵四边形ABCD是矩形,
∴AD∥BC,∠DAB=90°,
∴∠DAC=90°-30°-30°=30°,
∵四边形ABCD是矩形,
∴OA=OC,OB=OD,AC=BD,
∴OA=OB=OC=OD,
∵CH垂直平分线段OD,
∴CD=OC,
∴CD=OD=OC,
∴△DOC是等边三角形,
∵CG⊥BD,
∴∠DCG=∠ACG=30°,
∴∠DAC=∠ACG,
∴AH=CH,
∵AE⊥BD,CG⊥BD,
∴AF∥CH,
∵AD∥BC,
∴四边形AFCH是菱形.
点评:本题考查了线段垂直平分线性质,矩形的性质,平行四边形的判定,等腰三角形的判定,菱形的判定的应用,解此题的关键是推出四边形AFCH是平行四边形和求出AH=CH.

练习册系列答案
 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案
相关题目
青山村种的水稻2010年平均每公顷产7200kg,设水稻每公顷产量的年平均增长率为x,则2012年平均每公顷比2011年增加的产量是( )
| A、7200(x+1)2 kg |
| B、7200(x2+1)kg |
| C、7200(x2+x)kg |
| D、7200(x+1)kg |
设A、B为直线l上的两点,点P是直线l外的一点,若PA=3cm,PB=4cm,则点P到直线l的距离为( )
| A、等于3cm |
| B、小于3cm |
| C、不小于3cm |
| D、不大于3cm |
 如图,已知点A,B,C.请按要求作图:
如图,已知点A,B,C.请按要求作图: 如图,△ABC中,AB=AC,D是AB边的中点,E是AB延长线上一点,且BE=AB,则CD:CE=
如图,△ABC中,AB=AC,D是AB边的中点,E是AB延长线上一点,且BE=AB,则CD:CE= 如图,已知B、E分别是AC,DF上的点,且∠1=∠2,∠A=∠F
如图,已知B、E分别是AC,DF上的点,且∠1=∠2,∠A=∠F