题目内容
20.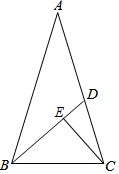 如图,在△ABC中,AB=AC,∠A=36°,∠ABC的平分线交AC于D,∠ACB的平分线交BD于点E,且CD=1,则DE的值为( )
如图,在△ABC中,AB=AC,∠A=36°,∠ABC的平分线交AC于D,∠ACB的平分线交BD于点E,且CD=1,则DE的值为( )| A. | $\frac{\sqrt{5}-1}{2}$ | B. | $\frac{\sqrt{5}+1}{2}$ | C. | $\frac{\sqrt{5}+3}{2}$ | D. | $\sqrt{5}-1$ |
分析 由等腰三角形的性质及角平分线的定义可求得BD=AD=BC,BE=CE=CD,由△BCD∽△ABC可求得BD的长,从而可求得DE.
解答 解:
∵AB=AC,∠A=36°,
∴∠ABC=∠ACB=72°,
∵BD平分∠ABC,CE平分∠ACB,
∴∠ABD=∠CBD=∠BCE=∠DCE=36°,
∴BD=BC=AD,CD=CE=BE=1,
∴BCD∽△ABC,
∴$\frac{CD}{BC}$=$\frac{BC}{AC}$,即$\frac{CD}{BD}$=$\frac{BD}{BD+CD}$,
∴$\frac{1}{BD}$=$\frac{BD}{BD+1}$,解得BD=$\frac{1+\sqrt{5}}{2}$,
∴DE=BD-BE=BD-CD=$\frac{\sqrt{5}+1}{2}$-1=$\frac{\sqrt{5}-1}{2}$,
故选A.
点评 本题主要考查等腰三角形的判定和性质,利用相似三角形的性质求得BD的长是解题的关键.

练习册系列答案
相关题目
15.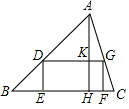 如图,△ABC中,点E、F在BC边上,点D,G分别在AB,AC边上,四边形DEFG是矩形,若矩形DEFG面积与△ADG的面积相等,设△ABC的BC边上高AH与DG相交于点K,则$\frac{DG}{BC}$的值为( )
如图,△ABC中,点E、F在BC边上,点D,G分别在AB,AC边上,四边形DEFG是矩形,若矩形DEFG面积与△ADG的面积相等,设△ABC的BC边上高AH与DG相交于点K,则$\frac{DG}{BC}$的值为( )
 如图,△ABC中,点E、F在BC边上,点D,G分别在AB,AC边上,四边形DEFG是矩形,若矩形DEFG面积与△ADG的面积相等,设△ABC的BC边上高AH与DG相交于点K,则$\frac{DG}{BC}$的值为( )
如图,△ABC中,点E、F在BC边上,点D,G分别在AB,AC边上,四边形DEFG是矩形,若矩形DEFG面积与△ADG的面积相等,设△ABC的BC边上高AH与DG相交于点K,则$\frac{DG}{BC}$的值为( )| A. | 1:1 | B. | 1:2 | C. | 2:3 | D. | $\sqrt{2}$:3 |
 如图所示,一棵大树高8米,一场大风过后,大树在离地面3米处折断倒下,树的顶端落在地上,则此时树的顶端离树的底部有( )米.
如图所示,一棵大树高8米,一场大风过后,大树在离地面3米处折断倒下,树的顶端落在地上,则此时树的顶端离树的底部有( )米.
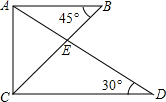 将一副三角尺如图所示叠放在一起,则$\frac{BE}{CE}$的值是$\frac{\sqrt{3}}{3}$.
将一副三角尺如图所示叠放在一起,则$\frac{BE}{CE}$的值是$\frac{\sqrt{3}}{3}$. 如图,在△ABC中,AB=AC=10,点D是BC边上的一动点(不与B、C重合),∠ADE=∠B=∠α,DE交AB于点E,且tan∠α=$\frac{3}{4}$,有以下的结论:①△DBE∽△ACD;②△ADE∽△ACD;③△BDE为直角三角形时,BD为8或$\frac{7}{2}$;④0<BE≤5,其中正确的结论是①③(填入正确结论的序号)
如图,在△ABC中,AB=AC=10,点D是BC边上的一动点(不与B、C重合),∠ADE=∠B=∠α,DE交AB于点E,且tan∠α=$\frac{3}{4}$,有以下的结论:①△DBE∽△ACD;②△ADE∽△ACD;③△BDE为直角三角形时,BD为8或$\frac{7}{2}$;④0<BE≤5,其中正确的结论是①③(填入正确结论的序号)