题目内容
若函数y=
与y=x+3的图象的交点坐标为(a,b),则
-
的值为 .
| 2 |
| x |
| 2 |
| a |
| 2 |
| b |
考点:反比例函数与一次函数的交点问题
专题:
分析:根据图象的交点坐标,可得方程组,根据解方程组,可得a,b的值,根据实数的运算,可得答案.
解答:解:由函数y=
与y=x+3的图象的交点坐标为(a,b),得
解得
或
.
当
时,
-
=
-
=
=
=3;
当
时,
-
=
-
=
=
=3;
故答案为:3.
| 2 |
| x |
|
解得
|
|
当
|
| 2 |
| a |
| 2 |
| b |
| 4 | ||
-3+
|
| 4 | ||
3+
|
4(3+
| ||||
(-3+
|
12+4
| ||||
| 17-9 |
当
|
| 2 |
| a |
| 2 |
| b |
| 4 | ||
-3-
|
| 4 | ||
3-
|
4(3-
| ||||
(-3-
|
12-4
| ||||
| 17-9 |
故答案为:3.
点评:本题考查了反比例函数与一次函数的交点问题,先求出交点坐标,再进行实数的运算.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
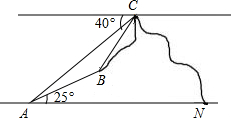 如图,MN表示水平地面,由地面上A处测得山上B处的仰角是25°,由山顶C处测得B处的俯角是40°.若AB:BC=2:3,求由A处测得C处的仰角(结果精确到0.1°).
如图,MN表示水平地面,由地面上A处测得山上B处的仰角是25°,由山顶C处测得B处的俯角是40°.若AB:BC=2:3,求由A处测得C处的仰角(结果精确到0.1°).