题目内容
7.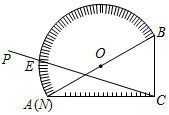 如图,量角器的直径与直角三角板ABC的斜边AB重合,其中量角器0刻度线的端点N与点A重合,射线CP从CA处出发沿顺时针方向以每秒2度的速度旋转,CP与量角器的半圆弧交于点E,第23秒时,点E在量角器上对应的度数是92度.
如图,量角器的直径与直角三角板ABC的斜边AB重合,其中量角器0刻度线的端点N与点A重合,射线CP从CA处出发沿顺时针方向以每秒2度的速度旋转,CP与量角器的半圆弧交于点E,第23秒时,点E在量角器上对应的度数是92度.
分析 先连接OE,由∠ACB=90°,根据圆周角定理,可得点C在⊙O上,即可得∠EOA=2∠ECA,又由∠ECA的度数,继而求得答案.
解答 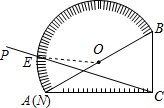 解:连接OE,
解:连接OE,
∵射线CP从CA处出发沿顺时针方向以每秒2度的速度旋转,
∴第23秒时,∠ACE=2°×23=46°,
∵∠ACB=90°,
∴点C在以AB为直径的圆上,
即点C在⊙O上,
∴∠EOA=2∠ECA=2×46°=92°.
故答案为:92.
点评 此题考查了圆周角定理,在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.解题的关键是证得点C在⊙O上,注意辅助线的作法以及数形结合思想的运用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
2. 如图,在△ABC中,AC=8,D、E分别为AB、AC的中点,F为线段DE上一点,连接AF、CF使AF⊥CF,且DF=1.若△ADF面积为2,则△ABC的面积为( )
如图,在△ABC中,AC=8,D、E分别为AB、AC的中点,F为线段DE上一点,连接AF、CF使AF⊥CF,且DF=1.若△ADF面积为2,则△ABC的面积为( )
 如图,在△ABC中,AC=8,D、E分别为AB、AC的中点,F为线段DE上一点,连接AF、CF使AF⊥CF,且DF=1.若△ADF面积为2,则△ABC的面积为( )
如图,在△ABC中,AC=8,D、E分别为AB、AC的中点,F为线段DE上一点,连接AF、CF使AF⊥CF,且DF=1.若△ADF面积为2,则△ABC的面积为( )| A. | 25 | B. | 30 | C. | 35 | D. | 40 |
12.将数字“69”旋转180°,得到的数字是( )
| A. | 96 | B. | 69 | C. | 66 | D. | 99 |
 如图,在△ABC中,∠A=50°,∠B=70°,点D在BC的延长线上,那么∠ACD=120°.
如图,在△ABC中,∠A=50°,∠B=70°,点D在BC的延长线上,那么∠ACD=120°.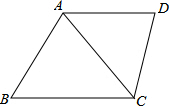 如图,梯形ABCD中,AD∥BC,AC为对角线,且∠DCA=∠B,线段AD、BC的长是方程x(x-4)+2(4-x)=0的两根,且AD<BC,CD=3,求AB与AC的长.
如图,梯形ABCD中,AD∥BC,AC为对角线,且∠DCA=∠B,线段AD、BC的长是方程x(x-4)+2(4-x)=0的两根,且AD<BC,CD=3,求AB与AC的长.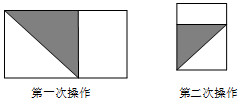 将长为1,宽为a的长方形纸片$({\frac{1}{2}<a<1})$如图那样折一下,剪下一个边长等于长方形的宽度的正方形(称为第一次操作);再把剩下的长方形如图那样折一下,剪下一个边长等于此时长方形宽度的正方形(称为第二次操作);如些反复操作下去,若在第n次操作后剩下的长方形为正方形,则操作终止.
将长为1,宽为a的长方形纸片$({\frac{1}{2}<a<1})$如图那样折一下,剪下一个边长等于长方形的宽度的正方形(称为第一次操作);再把剩下的长方形如图那样折一下,剪下一个边长等于此时长方形宽度的正方形(称为第二次操作);如些反复操作下去,若在第n次操作后剩下的长方形为正方形,则操作终止. 节约能源,保护生态,迎接低碳时代的到来,某纸品加工厂利用边角线裁出正方形和长方形两种硬纸片,制作甲、乙两种无盖的长方体纸盒出售给礼品店.
节约能源,保护生态,迎接低碳时代的到来,某纸品加工厂利用边角线裁出正方形和长方形两种硬纸片,制作甲、乙两种无盖的长方体纸盒出售给礼品店. 如图,点E在?ABCD的边AD上,沿BE折叠,点A落在边CD上的点F处,若△FDE的周长为8,△FCB的周长为22.求FC的长.
如图,点E在?ABCD的边AD上,沿BE折叠,点A落在边CD上的点F处,若△FDE的周长为8,△FCB的周长为22.求FC的长.