题目内容
13．
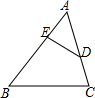如图，∠ADE=∠B，若AD：AB=2：3，则△ADE与△ABC的面积比为4：9．
分析 由∠A=∠A且∠ADE=∠B证△ADE∽△ABC得$\frac{{S}_{△ADE}}{{S}_{△ABC}}$=（$\frac{AD}{AB}$）2=$\frac{4}{9}$．
解答 解：∵∠A=∠A，且∠ADE=∠B，
∴△ADE∽△ABC，
∴$\frac{{S}_{△ADE}}{{S}_{△ABC}}$=（$\frac{AD}{AB}$）2=$\frac{4}{9}$，
故答案为：4：9．
点评 本题主要考查相似三角形的判定与性质，熟练掌握相似三角形的面积比等于相似比的平方是解题的关键．
练习册系列答案
相关题目
1．某市为美化城市，有关部门决定利用现有的4200盆甲种花卉和3090盆乙种花卉，搭配成A、B两种园艺造型共60个，摆放于主干街道的两侧，搭配每个造型所需花卉数量的情况如下表所示，结合上述信息，解答下列问题：
（1）符合题意的搭配方案有几种？
（2）如果搭配一个A种造型的成本为600元，搭配一个B种造型的成本为800元，试说明选用那种方案成本最低？最低成本为多少元？
| 造型花卉 | 甲 | 乙 |
| A | 80 | 40 |
| B | 50 | 70 |
（2）如果搭配一个A种造型的成本为600元，搭配一个B种造型的成本为800元，试说明选用那种方案成本最低？最低成本为多少元？
如图，在△ABC中，∠A=50°，∠B=70°，点D在BC的延长线上，那么∠ACD=120°．
如图，在△ABC中，AC=8，D、E分别为AB、AC的中点，F为线段DE上一点，连接AF、CF使AF⊥CF，且DF=1．若△ADF面积为2，则△ABC的面积为（ ）