题目内容
5. 如图,△ABC在直角坐标系中
如图,△ABC在直角坐标系中(1)点A坐标为(-2,-2),点C坐标为(0,2 ).
(2)若把△ABC向上平移2个单位,再向左平移1个单位得到△A′B′C′,画出平移后的图形.
(3)三角形ABC的面积是7.
分析 (1)根据直角坐标系的特点写出点A、C的坐标;
(2)分别将点A、B、C向上平移2个单位,再向左平移1个单位,然后顺次连接;
(3)用三角形ABC所在的矩形的面积减去三个小三角形的面积即可得解.
解答 解:(1)A(-2,-2),C(0,2);
(2)所作图形如图所示:
(3)S△ABC=4×5-$\frac{1}{2}$×2×4-$\frac{1}{2}$×3×5-$\frac{1}{2}$×1×3
=7.
故答案为:-2,-2,0,2;7.
点评 本题考查了根据平移变换作图,解答本题的关键是根据网格结构作出对应点的位置,然后顺次连接.

练习册系列答案
相关题目
16.对于方程:3x+2y=4,下列说法正确的是( )
| A. | 无正数解 | B. | 只有一组正数解 | ||
| C. | 无正整数解 | D. | 只有一组正整数解 |
13.若方程ax2+bx+c=0(a≠0)中,a,b,c满足a+b+c=0和a-b+c=0,则方程的根是( )
| A. | 1,0 | B. | -1,0 | C. | 1,-1 | D. | 无法确定 |
17.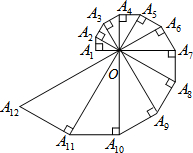 如图,已知A1A2=1,∠OA1A2=90°,∠A1OA2=30°,以斜边OA2为直角边作直角三角形,使得∠A2OA3=30°,依次以前一个直角三角形的斜边为直角边一直作含30°角的直角三角形,则Rt△A2014OA2015的最小边长为( )
如图,已知A1A2=1,∠OA1A2=90°,∠A1OA2=30°,以斜边OA2为直角边作直角三角形,使得∠A2OA3=30°,依次以前一个直角三角形的斜边为直角边一直作含30°角的直角三角形,则Rt△A2014OA2015的最小边长为( )
 如图,已知A1A2=1,∠OA1A2=90°,∠A1OA2=30°,以斜边OA2为直角边作直角三角形,使得∠A2OA3=30°,依次以前一个直角三角形的斜边为直角边一直作含30°角的直角三角形,则Rt△A2014OA2015的最小边长为( )
如图,已知A1A2=1,∠OA1A2=90°,∠A1OA2=30°,以斜边OA2为直角边作直角三角形,使得∠A2OA3=30°,依次以前一个直角三角形的斜边为直角边一直作含30°角的直角三角形,则Rt△A2014OA2015的最小边长为( )| A. | 22013 | B. | 22014 | C. | ($\frac{2}{\sqrt{3}}$)2013 | D. | ($\frac{2}{\sqrt{3}}$)2014 |
 如图,已知扇形的圆心角为60°,半径为$\sqrt{3}$,则图中弓形的面积为$\frac{2π-3\sqrt{3}}{4}$.
如图,已知扇形的圆心角为60°,半径为$\sqrt{3}$,则图中弓形的面积为$\frac{2π-3\sqrt{3}}{4}$.