题目内容
14.(1)已知x2-4x-1=0,求代数式(2x-3)2-(x+y)(x-y)-y2的值.(2)先化简($\frac{{x}^{2}}{x-1}$-x+1)÷$\frac{4{x}^{2}-4x+1}{1-x}$,再选一个你喜欢的数代入求值;
(3)已知方程$\frac{1}{x-1}$=$\frac{a}{x+1}$的解为x=2,求a的值.
分析 (1)先算乘法,再合并同类项,变形后代入求出即可;
(2)先算减法,同时把除法变成乘法,再根据分式的乘法法则求出即可;
(3)把x=2代入方程,即可求出答案.
解答 解:(1)∵x2-4x-1=0,
∴x2-4x=1,
∴(2x-3)2-(x+y)(x-y)-y2
=4x2-12x+9-x2+y2-y2
=3x2-12x+9
=3(x2-4x)+9
=12;
(2)原式=$\frac{{x}^{2}-(x-1)^{2}}{x-1}$•$\frac{1-x}{(2x-1)^{2}}$
=$\frac{2x-1}{x-1}$•$\frac{-(x-1)}{(2x-1)^{2}}$
=$\frac{1}{1-2x}$,
取x=0时,原式=-1;
(3)因为此方程的解为x=2,
所以把x=2代入$\frac{1}{x-1}$=$\frac{a}{x+1}$中得:1=$\frac{1}{3}$a,
解得:x=3.
点评 本题考查了整式的混合运算和求值,分式的混合运算,解分式方程等知识点,能灵活运用知识点进行计算是解此题的关键,注意:运算顺序.

练习册系列答案
相关题目
5.在同一平面内,下列说法正确的是( )
| A. | 两点之间的距离就是两点间的线段 | |
| B. | 与同一条直线垂直的两条直线也垂直 | |
| C. | 过一点有且只有一条直线与已知直线平行 | |
| D. | 过一点有且只有一条直线与已知直线垂直 |
4.下列计算正确的是( )
| A. | $\sqrt{4}=±2$ | B. | $2\sqrt{3}=\sqrt{6}$ | C. | $2+\sqrt{3}=3\sqrt{3}$ | D. | $\sqrt{8}-\sqrt{2}=\sqrt{2}$ |

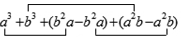
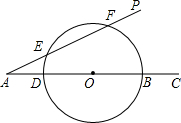 如图:∠PAC=30°,AD=3,BD=10,以BD为直径的交AP于E、F,求圆心O到AP的距离及EF长.
如图:∠PAC=30°,AD=3,BD=10,以BD为直径的交AP于E、F,求圆心O到AP的距离及EF长. 画一画
画一画