题目内容
3.我国古代数学的许多发现都位居世界前列,其中“杨辉三角”就是一例,如图所示,它给出了(a+b)n(n为非负整数)的展开式(按a的次数由大到小的顺序排列)的系数规律,例如:1(a+b)0=1
11(a+b)1=a+b
121(a+b)2=a2+2ab+b2
1331(a+b)3=a3+3a2b+3ab2+b3
14641(a+b)4=a4+4a3b+6a2b2+4ab3+b4
(1)请利用以上规律,写出(a+b)5的展开式的系数.
(a+b)5=1a5+5a4b+10a3b2+10a2b3+5ab4+1b5.
(2)请利用以上规律计算下列式子的值;
①-2×35+10×34-20×33+20×32-10×3+2=-64.
②36-5×35+10×34-10×33+5×32-3=160.
(3)请利用以上规律求出(2x-1)6展开式中a1+a2+a5的值.
(2x-1)6=a6x6+a5x5+a4x4+a3x3+a2x2+a1x+a0.
分析 (1)结合题意画出对应“杨辉三角”,根据图形可得结果;
(2)①提取-2后,可得原式=-2[35+5×34×(-1)+10×33×(-1)2+10×32×(-1)3+5×3×(-1)4+(-1)5]=-2×(3-1)5,可得答案;
②提取3后,得原式=3[35+5×34×(-1)+10×33×(-1)2+10×32×(-1)3+5×3×(-1)4+(-1)5]=3×(3-1)5,可得答案;
(3)利用以上规律,得(2x-1)6=(2x)6+6×(2x)5×(-1)+15×(2x)4×(-1)2+20×(2x)3×(-1)3+15×(2x)2×(-1)4+6×(2x)×(-1)5+(-1)6,计算a1+a2+a5可得答案.
解答 解:(1)如图,
则(a+b)5=a5+5a4b+10a3b2+10a2b3+5ab4+b5;
故答案为:1、5、10、10、5、5、1;
(2)①原式=-2[35+5×34×(-1)+10×33×(-1)2+10×32×(-1)3+5×3×(-1)4+(-1)5]=-2×(3-1)5=-2×25=-64;
②原式=3(35-5×34+10×33-10×32+5×3-1)
=3[35+5×34×(-1)+10×33×(-1)2+10×32×(-1)3+5×3×(-1)4+(-1)5]
=3×(3-1)5
=3×25
=160,
故答案为:-64、160;
(3)∵(2x-1)6=(2x)6+6×(2x)5×(-1)+15×(2x)4×(-1)2+20×(2x)3×(-1)3+15×(2x)2×(-1)4+6×(2x)×(-1)5+(-1)6,
∴a1+a2+a5=6×2×(-1)5+15×22×(-1)4+6×25×(-1)=-12+60-192=-144.
点评 本题考查了完全式的n次方,也是数字类的规律题,首先根据图形中数字找出对应的规律,再表示展开式:对应(a+b)n中,相同字母a的指数是从高到低,相同字母b的指数是从低到高.

 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案| A. | 相等 | B. | 互为倒数 | C. | 互为相反数 | D. | 不能确定 |
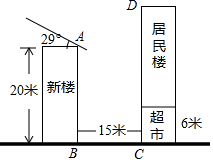 某居民小区有一朝向为正南方向的居民楼.该居民楼的一楼是高6米的小区超市,超市以上是居民住房.在该楼前面15米处要盖一栋高20米的新楼.已知上海地区冬至正午的阳光与水平线夹角为29°.(参考数据:sin29°≈0.48;cos29°≈0.87;tan29°≈0.55)
某居民小区有一朝向为正南方向的居民楼.该居民楼的一楼是高6米的小区超市,超市以上是居民住房.在该楼前面15米处要盖一栋高20米的新楼.已知上海地区冬至正午的阳光与水平线夹角为29°.(参考数据:sin29°≈0.48;cos29°≈0.87;tan29°≈0.55)