题目内容
在实数的原有运算法则中我们补充定义新运算“⊕”如下:当a≥b时,a⊕b=b2,当a<b时,a⊕b=ab.
(1)计算:-5⊕8;
(2)当x=2时,求(1⊕x)⊕(3⊕x)的值.
(1)计算:-5⊕8;
(2)当x=2时,求(1⊕x)⊕(3⊕x)的值.
考点:实数的运算
专题:新定义
分析:(1)根据当a≥b时,a⊕b=b2,当a<b时,a⊕b=ab得出即可;
(2)分别化简原式,进而求出答案.
(2)分别化简原式,进而求出答案.
解答:解:(1)-5⊕8=-5×8=-40;
(2)当x=2时,
1⊕x=1⊕2=2;
3⊕x=3⊕2=4,
故(1⊕x)⊕(3⊕x)=2×4=8.
(2)当x=2时,
1⊕x=1⊕2=2;
3⊕x=3⊕2=4,
故(1⊕x)⊕(3⊕x)=2×4=8.
点评:此题主要考查了实数的运算,正确根据题意化简得出是解题关键.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
 如图为手的示意图,从大拇指开始,按食指,中指,无名指,小指,再回到大拇指的顺序,依次数正整数1,2,3,4,5当数到2015时,对应的手指( )
如图为手的示意图,从大拇指开始,按食指,中指,无名指,小指,再回到大拇指的顺序,依次数正整数1,2,3,4,5当数到2015时,对应的手指( )| A、食指 | B、中指 | C、无名指 | D、小指 |
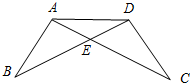 在一次数学课上,王老师在黑板上画出一幅图,并写下了四个等式:
在一次数学课上,王老师在黑板上画出一幅图,并写下了四个等式: 如图,若△OAD≌△OBC,且∠O=65°,∠C=20°,求∠OAD的度数.
如图,若△OAD≌△OBC,且∠O=65°,∠C=20°,求∠OAD的度数.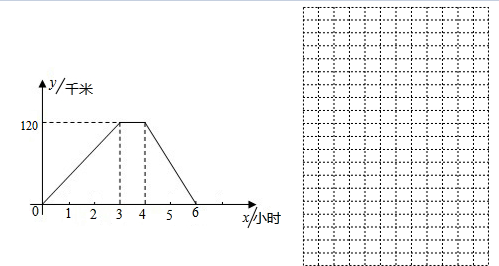
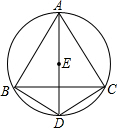 如图,四边形ABDC是圆内接四边形,E是AD上一点,且是△ABC的内心.求证:DB=DE=DC.
如图,四边形ABDC是圆内接四边形,E是AD上一点,且是△ABC的内心.求证:DB=DE=DC.