题目内容
 如图,在Rt△ABC中,∠BAC=90°,∠BAC的平分线交BC于点O,以O为圆心做圆,⊙O与AC相切于点D.
如图,在Rt△ABC中,∠BAC=90°,∠BAC的平分线交BC于点O,以O为圆心做圆,⊙O与AC相切于点D.(1)试判断AB与⊙O的位置关系,并加以证明.
(2)在Rt△ABC中,若AC=6,AB=3,求切线AD的长.
考点:切线的判定,切线的性质
专题:
分析:(1)过点O作OE⊥AB,垂足为E,连接OD,根据角平分线的性质可得出OE=OD,继而可得出结论;
(2)根据S△ABC=S△AOC+S△BOC,可得出⊙O的半径,从而得出切线AD的长.
(2)根据S△ABC=S△AOC+S△BOC,可得出⊙O的半径,从而得出切线AD的长.
解答: 证明:(1)过点O作OE⊥BA,垂足为E,连接OD,
证明:(1)过点O作OE⊥BA,垂足为E,连接OD,
∵AC是圆的切线,
∴OD⊥AC,
又∵OC为∠BAC的平分线,
∴OE=OD,即OE是⊙O的半径,
∴BA与⊙0相切;
(2)设⊙O的半径为r,
∵S△ABC=S△AOC+S△BOA,
∴
AC×BA=
AC×OD+
BA×OE,
∵OE=OD=r,AC=6,AB=3,
∴r(AC+BA)=18,
即9r=18,
解得:r=2.
∵∠DAO=∠DOA=45°,
∴AD=OD=r,
即AD的长为2.
 证明:(1)过点O作OE⊥BA,垂足为E,连接OD,
证明:(1)过点O作OE⊥BA,垂足为E,连接OD,∵AC是圆的切线,
∴OD⊥AC,
又∵OC为∠BAC的平分线,
∴OE=OD,即OE是⊙O的半径,
∴BA与⊙0相切;
(2)设⊙O的半径为r,
∵S△ABC=S△AOC+S△BOA,
∴
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∵OE=OD=r,AC=6,AB=3,
∴r(AC+BA)=18,
即9r=18,
解得:r=2.
∵∠DAO=∠DOA=45°,
∴AD=OD=r,
即AD的长为2.
点评:本题考查了切线的判定及性质,利用等积法求圆的半径是很巧妙的方法,也比较重要,希望同学们认真掌握.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图为手的示意图,从大拇指开始,按食指,中指,无名指,小指,再回到大拇指的顺序,依次数正整数1,2,3,4,5当数到2015时,对应的手指( )
如图为手的示意图,从大拇指开始,按食指,中指,无名指,小指,再回到大拇指的顺序,依次数正整数1,2,3,4,5当数到2015时,对应的手指( )| A、食指 | B、中指 | C、无名指 | D、小指 |
当x=2时,代数式ax2+bx3+cx-2的值是2013,则当x=-2时,代数式-ax2+bx3+cx-2的值为( )
| A、-2017 | B、2011 |
| C、-2013 | D、2017 |
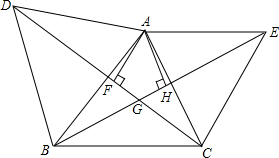 如图,已知△ABD、△AEC都是等边三角形,AF⊥CD于F,AH⊥BE于H.
如图,已知△ABD、△AEC都是等边三角形,AF⊥CD于F,AH⊥BE于H.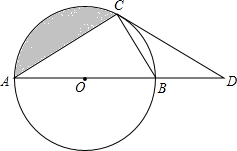 如图,AB是⊙O的直径,C为⊙O上一点,点D在AB的延长线上,∠DCB=∠A.
如图,AB是⊙O的直径,C为⊙O上一点,点D在AB的延长线上,∠DCB=∠A.  如图,在三角形ABC中,点D,E,F分别在BC,AB,AC上,BD=CF,BE=CD,AB=AC,DG⊥EF于点G,求证:EG=FG.
如图,在三角形ABC中,点D,E,F分别在BC,AB,AC上,BD=CF,BE=CD,AB=AC,DG⊥EF于点G,求证:EG=FG.