题目内容
14.下列根式中,与$\sqrt{2}$是同类二次根式的是( )| A. | $\sqrt{12}$ | B. | $\sqrt{8}$ | C. | $\sqrt{6}$ | D. | $\sqrt{3}$ |
分析 把各选项中式子化为最简二次根式,利用同类二次根式定义判断即可.
解答 解:A、$\sqrt{12}$=2$\sqrt{3}$,与$\sqrt{2}$不是同类二次根式;
B、$\sqrt{8}$=2$\sqrt{2}$,与$\sqrt{2}$是同类二次根式;
C、$\sqrt{6}$与$\sqrt{2}$不是同类二次根式;
D、$\sqrt{3}$与$\sqrt{2}$不是同类二次根式,
故选B
点评 此题考查了同类二次根式,以及最简二次根式,熟练掌握同类二次根式定义是解本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
4.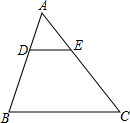 如图,在△ABC中,点D、E分别在边AB、AC上,AD:DB=2:3,∠B=∠ADE,则DE:BC等于( )
如图,在△ABC中,点D、E分别在边AB、AC上,AD:DB=2:3,∠B=∠ADE,则DE:BC等于( )
 如图,在△ABC中,点D、E分别在边AB、AC上,AD:DB=2:3,∠B=∠ADE,则DE:BC等于( )
如图,在△ABC中,点D、E分别在边AB、AC上,AD:DB=2:3,∠B=∠ADE,则DE:BC等于( )| A. | 1:2 | B. | 1:3 | C. | 2:3 | D. | 2:5 |
2.下列命题中:
①同位角相等,两直线平行;
②在△ABC中,a,b,c分别是∠A、∠B、∠C的对边,如果∠C=90°,那么a2+b2=c2;
③菱形是对角线互相垂直的四边形;
④矩形是对角线相等的平行四边形.
它们的逆命题是真命题的有( )
①同位角相等,两直线平行;
②在△ABC中,a,b,c分别是∠A、∠B、∠C的对边,如果∠C=90°,那么a2+b2=c2;
③菱形是对角线互相垂直的四边形;
④矩形是对角线相等的平行四边形.
它们的逆命题是真命题的有( )
| A. | ①②③ | B. | ①②④ | C. | ①③④ | D. | ②③④ |
9.若点P(2014,a)、Q(2015,b)都在函数y=$\frac{2016}{x}$的图象上,则下列结论中正确的是( )
| A. | a>b | B. | a=b | ||
| C. | a<b | D. | a、b的大小关系无法确定 |
19.已知一次函数y=-x+b,过点(-8,-2),那么一次函数的解析式为( )
| A. | y=-x-2 | B. | y=-x-6 | C. | y=-x-10 | D. | y=-x-1 |
6.若m>n,则下列各式正确的是( )
| A. | m+4<n+4 | B. | 6m<6n | C. | -5m<-5n | D. | 3m-1<3n-1 |
3.命题:“关于x的一元二次方程x2+bx+1=0,当b<0时,必有实数根”;能说明这个命题是假命题的一个反例可以是( )
| A. | b=-1 | B. | b=-2 | C. | b=-3 | D. | b=-4 |
4.若五个正整数的中位数是3,且唯一的众数是7,则这五个数的平均数是( )
| A. | 4 | B. | 5 | C. | 6 | D. | 8 |