题目内容
9.若实数a、b、c满足$\sqrt{b-2a+3}+|a+b-2|$=$\sqrt{c-2}+\sqrt{2-c}$,则$\sqrt{{a}^{2}+{b}^{2}+{c}^{2}}$的值为$\frac{\sqrt{182}}{3}$.分析 由二次根式的定义得到c的值.然后由非负数的性质可以求得a、b的值;最后将其代入所求的代数式进行求值.
解答 解:依题意得:c=2,
则$\left\{\begin{array}{l}{b-2a+3=0}\\{a+b-2=0}\end{array}\right.$,
解得$\left\{\begin{array}{l}{a=-\frac{5}{3}}\\{b=\frac{11}{3}}\end{array}\right.$,
所以$\sqrt{{a}^{2}+{b}^{2}+{c}^{2}}$=$\sqrt{\frac{25}{9}+\frac{121}{9}+4}$=$\frac{\sqrt{182}}{3}$.
故答案是:$\frac{\sqrt{182}}{3}$.
点评 考查了二次根式的意义和性质.概念:式子$\sqrt{a}$(a≥0)叫二次根式.性质:二次根式中的被开方数必须是非负数,否则二次根式无意义.同时考查了非负数的性质,几个非负数的和为0,这几个非负数都为0.

练习册系列答案
相关题目
19.已知y=ax2+k的图象上有三点A(-3,y1),B(1,y2),C(2,y3),且y2<y3<y1,则a的取值范围是( )
| A. | a>0 | B. | a<0 | C. | a≥0 | D. | a≤0 |
7.CD为△ABC的高且∠A:∠B:∠C=1:2:3,AB=m,则CD等于( )
| A. | $\frac{m}{2}$ | B. | $\frac{m}{4}$ | C. | $\frac{\sqrt{3}}{4}$m | D. | $\frac{\sqrt{3}}{2}$m |

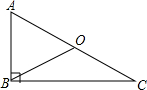 如图,已知Rt△ABC,∠ABC=90°,BO是斜边AC上的中线.
如图,已知Rt△ABC,∠ABC=90°,BO是斜边AC上的中线.