题目内容
4.在墙边(足够长)的空地上,准备用36m长的篱笆围一块长方形花圃,问长是多少时,才能使围成的面积最大,最大面积是多少?分析 设长方形花圃的长是xm,则宽为($\frac{36}{2}$-x)m,面积为S,由题意列出函数,利用配方求得最大值即可.
解答 解:设长方形花圃的长是xm,则宽为($\frac{36}{2}$-x)m,面积为S,
则S=x($\frac{36}{2}$-x)
=-x2+18x
=-(x-9)2+81
即长是9m时,才能使围成的面积最大,最大面积是81m2.
点评 此题考查二次函数的最值,利用长方形的面积计算公式列出二次函数是解决问题的关键.

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案
相关题目
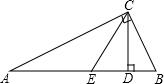 如图,在Rt△ABC中,已知∠ACB=90°,BC=2$\sqrt{3}$,CD⊥AB,垂足为点D,CD,CE三等分∠ACB,求△ACE的周长.
如图,在Rt△ABC中,已知∠ACB=90°,BC=2$\sqrt{3}$,CD⊥AB,垂足为点D,CD,CE三等分∠ACB,求△ACE的周长.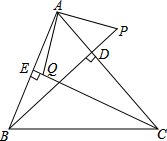 如图,已知BD、CE是△ABC的两条高,点P在BD的延长线上,点Q在CE上,且BP=AC,AB=CQ.求证:AP⊥AQ.
如图,已知BD、CE是△ABC的两条高,点P在BD的延长线上,点Q在CE上,且BP=AC,AB=CQ.求证:AP⊥AQ.