题目内容
9.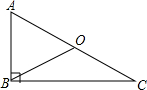 如图,已知Rt△ABC,∠ABC=90°,BO是斜边AC上的中线.
如图,已知Rt△ABC,∠ABC=90°,BO是斜边AC上的中线.(1)若BO=3cm,则AC=6cm;
(2)若BO=6.5cm,AB=5cm,则BC=12cm.
分析 (1)根据直角三角形斜边上的中线等于斜边的一半即可得出AC=2BO=6cm;
(2)先根据直角三角形斜边上的中线等于斜边的一半得出AC=2BO=13cm,然后利用勾股定理即可求解.
解答 解:(1)∵Rt△ABC,∠ABC=90°,BO是斜边AC上的中线,BO=3cm,
∴AC=2BO=6cm;
(2)∵Rt△ABC,∠ABC=90°,BO是斜边AC上的中线,BO=6.5cm,
∴AC=2BO=13cm,
又∵AB=5cm,
∴BC=$\sqrt{A{C}^{2}-A{B}^{2}}$=$\sqrt{1{3}^{2}-{5}^{2}}$=12(cm).
故答案为6;12.
点评 本题考查了直角三角形斜边上的中线的性质以及勾股定理,掌握在直角三角形中,斜边上的中线等于斜边的一半是解题的关键.

练习册系列答案
相关题目
19.某种商品每件的进价为190元,按标准的九折销售时.利润率为15.2%,设这种商品的标价为每件x元,依题意列方程正确的是( )
| A. | 0.9x-190=190×0.152 | B. | 0.9x=190×0.152 | ||
| C. | 0.152x=190×0.9 | D. | 190-0.9x=190×0.152 |
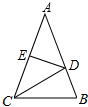 如图,在△ABC中,DE是AC的垂直平分线,分别交AB、AC于D、E两点.
如图,在△ABC中,DE是AC的垂直平分线,分别交AB、AC于D、E两点.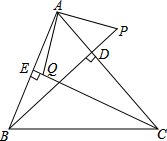 如图,已知BD、CE是△ABC的两条高,点P在BD的延长线上,点Q在CE上,且BP=AC,AB=CQ.求证:AP⊥AQ.
如图,已知BD、CE是△ABC的两条高,点P在BD的延长线上,点Q在CE上,且BP=AC,AB=CQ.求证:AP⊥AQ. 写出下列各函数的表达式.指出它是什么函数,并确定函数的自变量的取值范围.
写出下列各函数的表达式.指出它是什么函数,并确定函数的自变量的取值范围.