题目内容
19.已知y=ax2+k的图象上有三点A(-3,y1),B(1,y2),C(2,y3),且y2<y3<y1,则a的取值范围是( )| A. | a>0 | B. | a<0 | C. | a≥0 | D. | a≤0 |
分析 先根据二次函数图象上点的坐标特征可计算出y1=9a+k,y2=a+k,y3=4a+k,再利用y2<y3<y1得a+k<4a+k<9a+k,然后解不等式即可得到a的取值范围.
解答 解:∵点A(-3,y1),B(1,y2),C(2,y3)在抛物线y=ax2+k上,
∴y1=a•(-3)2+k=9a+k,y2=a•12+k=a+k,y3=a•22+k=4a+k,
∵y2<y3<y1,
∴a+k<4a+k<9a+k,
∴a>0.
故选A.
点评 本题考查了二次函数图象上点的坐标特征:二次函数图象上点的坐标满足其解析式.

练习册系列答案
相关题目
7.计算(a+2)2(a2+4)2(a-2)2的结果是( )
| A. | a8-64 | B. | a8-256 | C. | a8-16a4+64 | D. | a8-32a4+256 |
4.下列各组条件,不能判定△ABC与△A′B′C′相似的是( )
| A. | ∠A=∠A′∠B=∠B′ | B. | ∠C=∠C′=90°,∠A=12°,∠B=78° | ||
| C. | ∠A=∠B,∠B′=∠A′ | D. | ∠A+∠B=∠A′+∠B′,∠A-∠B=∠A′-∠B′ |
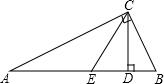 如图,在Rt△ABC中,已知∠ACB=90°,BC=2$\sqrt{3}$,CD⊥AB,垂足为点D,CD,CE三等分∠ACB,求△ACE的周长.
如图,在Rt△ABC中,已知∠ACB=90°,BC=2$\sqrt{3}$,CD⊥AB,垂足为点D,CD,CE三等分∠ACB,求△ACE的周长.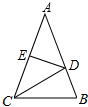 如图,在△ABC中,DE是AC的垂直平分线,分别交AB、AC于D、E两点.
如图,在△ABC中,DE是AC的垂直平分线,分别交AB、AC于D、E两点.