题目内容
20.根据下列条件.判断△ABC的形状(按角分类).(1)∠A=80°,∠B=25°
(2)∠A:∠B:∠C=1:2:3;
(3)∠A=$\frac{1}{2}$∠B=$\frac{1}{6}$∠C.
分析 (1)直接根据三角形内角和定理求出∠C的度数,进而可得出结论;
(2)设∠A=x,则∠B=2x,∠C=3x,再由三角形内角和定理求出x的值,进而得出∠C的值,由此可得出结论;
(3)设∠A=x,则∠B=2x,∠C=6x,再由三角形内角和定理求出x的值,进而得出∠C的值,由此可得出结论.
解答 解:(1)∵∠A=80°,∠B=25°,
∴∠C=180°-80°-25°=75°,
∴△ABC是锐角三角形;
(2)设∠A=x,则∠B=2x,∠C=3x,
∵∠A+∠B+∠C=180°,即x+2x+3x=180°,解得x=30°,
∴∠C=3x=90°,
∴△ABC是直角三角形;
(3)设∠A=x,则∠B=2x,∠C=6x,
∵∠A+∠B+∠C=180°,即x+2x+6x=180°,解得x=20°,
∴∠C=6x=120°,
∴△ABC是钝角三角形.
点评 本题考查的是三角形内角和定理,熟知三角形内角和是180°是解答此题的关键.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
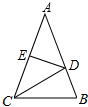 如图,在△ABC中,DE是AC的垂直平分线,分别交AB、AC于D、E两点.
如图,在△ABC中,DE是AC的垂直平分线,分别交AB、AC于D、E两点. 写出下列各函数的表达式.指出它是什么函数,并确定函数的自变量的取值范围.
写出下列各函数的表达式.指出它是什么函数,并确定函数的自变量的取值范围.