Question

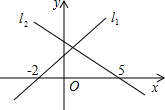如图，在同一平面直角坐标系内，直线l₁：y=kx+b与直线l₂：y=mx+n分别与x轴交于点（-2，0）与（5，0），则不等式组

kx+b＜0 mx+n＞0

的解集为（　　）

• A、x＜-2
• B、x＞5
• C、-2＜x＜5
• D、无解

Answer 1

考点：一次函数与一元一次不等式

专题：

分析：观察函数图象得到在x轴上-2的左边，对应于每一个x的值，函数值y=kx+b都落在x轴的下方，即不等式kx+b＜0的解集为x＜-2；在x轴上5的左边，对应于每一个x的值，函数值y=mx+n都落在x轴的上方，即不等式mx+n＞0的解集为x＜5；再根据“同小取较小”即可得出不等式组

kx+b＜0 mx+n＞0

的解集．

解答：解：观察函数图象得到
不等式kx+b＜0的解集为x＜-2，
不等式mx+n＞0的解集为x＜5；
所以不等式组

kx+b＜0 mx+n＞0

的解集为x＜-2．
故选A．

点评：本题考查了一次函数与一元一次不等式：观察函数图象，确定直线y=kx+b在x轴上（或下）方部分所有的点的横坐标所构成的集合，就是kx+b＞0（或＜0）的解集，也考查了一元一次不等式组的解法及数形结合的思想．