题目内容
如图，点P与正方形ABCD的四个顶点都在⊙O的圆周上，则∠APB=（ ）| A、30° | B、45° |
| C、60° | D、90° |
考点：圆周角定理
专题：计算题
分析：连结BD，根据正方形的性质∠ADB=45°，然后根据圆周角定理求解．
解答：
解：连结BD，如图，
∵四边形ABCD为正方形，
∴∠ADB=45°，
∴∠APB=∠ADB=45°．
故选B．
解：连结BD，如图，∵四边形ABCD为正方形，
∴∠ADB=45°，
∴∠APB=∠ADB=45°．
故选B．
点评：本题考查了圆周角定理：在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半．也考查了正方形的性质．
练习册系列答案
相关题目
点A（2，3）向左平移3个单位长度得到点A′，则点A′的坐标为（ ）
| A、（2，0） |
| B、（-1，3） |
| C、（-2，3） |
| D、（5，3） |
已知⊙O1和⊙O2的半径分别为3和5，圆心距O1O2=2，则⊙O1和⊙O2的位置关系是（ ）
| A、外离 | B、外切 | C、相交 | D、内切 |
如图，Rt△ABO的斜边AB=4，∠A=30°，将△ABO绕点O顺时针旋转90°至三角板A′B′O的位置，再沿OB方向平移，使点B′落在反比例函数y=| -6 |
| x |
| A、4cm | ||
B、2
| ||
| C、3cm | ||
D、（4，2
|
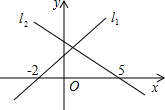如图，在同一平面直角坐标系内，直线l1：y=kx+b与直线l2：y=mx+n分别与x轴交于点（-2，0）与（5，0），则不等式组
|
| A、x＜-2 | B、x＞5 |
| C、-2＜x＜5 | D、无解 |
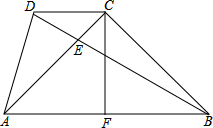已知：如图，点C是等腰直角△ABC的直角顶点，DC∥AB，BD=AB，BD交AC于点E，CF⊥AB，垂足为F，求证：