题目内容
 如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.
如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.(1)求证:△ADF∽△DEC;
(2)若AB=4,AD=3
| 3 |
(3)若CD=CE,则直线CD是以点E为圆心,AE长为半径的圆的切线.试证明之.
考点:相似三角形的判定与性质,勾股定理,平行四边形的性质,切线的判定
专题:
分析:(1)根据四边形ABCD是平行四边形,得出AB∥CD,AD∥BC,再根据平行线的性质得出∠B+∠C=180°,∠ADF=∠DEC,然后根据∠AFD+∠AFE=180°,
∠AFE=∠B,得出∠AFD=∠C,从而得出△ADF∽△DEC;
(2)根据已知和勾股定理得出DE=
,再根据△ADF∽△DEC,得出
=
,即可求出AF的长;
(3)先过点E作EH⊥CD于点H,在△ADE和△HDE中,根据AAS得出△ADE≌△HDE,AE=HE,即可得出直线CD是以点E为圆心,AE长为半径的圆的切线.
∠AFE=∠B,得出∠AFD=∠C,从而得出△ADF∽△DEC;
(2)根据已知和勾股定理得出DE=
| AD2+AE2 |
| AF |
| DC |
| AD |
| DE |
(3)先过点E作EH⊥CD于点H,在△ADE和△HDE中,根据AAS得出△ADE≌△HDE,AE=HE,即可得出直线CD是以点E为圆心,AE长为半径的圆的切线.
解答:解:(1)∵四边形ABCD是平行四边形,
∴AB∥CD,AD∥BC,
∴∠B+∠C=180°,∠ADF=∠DEC,
∵∠AFD+∠AFE=180°,∠AFE=∠B,
∴∠AFD=∠C,
∴△ADF∽△DEC;
(2)∵AE⊥BC,AD=3
,AE=3,
∴DE=
=
=6,
由(1)知△ADF∽△DEC,得
=
,
∴AF=
=
=2
.
(3)过点E作EH⊥CD于点H.
∵CD=CE,
∴∠CED=∠CDE.
∵∠ADE=∠CED,
∴∠ADE=∠CDE.
又∵∠EAD=∠EHD=90°,DE=DE,
在△ADE和△HDE中,
∴△ADE≌△HDE,
∴AE=HE,
∴直线CD是以点E为圆心,AE长为半径的圆的切线.
∴AB∥CD,AD∥BC,
∴∠B+∠C=180°,∠ADF=∠DEC,
∵∠AFD+∠AFE=180°,∠AFE=∠B,
∴∠AFD=∠C,
∴△ADF∽△DEC;
(2)∵AE⊥BC,AD=3
| 3 |
∴DE=
| AD2+AE2 |
(3
|
由(1)知△ADF∽△DEC,得
| AF |
| DC |
| AD |
| DE |
∴AF=
| DC×AD |
| DE |
4×3
| ||
| 6 |
| 3 |
(3)过点E作EH⊥CD于点H.

∵CD=CE,
∴∠CED=∠CDE.
∵∠ADE=∠CED,
∴∠ADE=∠CDE.
又∵∠EAD=∠EHD=90°,DE=DE,
在△ADE和△HDE中,
|
∴△ADE≌△HDE,
∴AE=HE,
∴直线CD是以点E为圆心,AE长为半径的圆的切线.
点评:此题考查了相似形的综合,用到的知识点是平行四边形的性质、相似三角形的判定与性质、切线的判定、勾股定理,关键是根据题意画出图形,构造直角三角形.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
 如图,在Rt△ABC中,∠C=90°,AC=15,BC=8,则sinA=( )
如图,在Rt△ABC中,∠C=90°,AC=15,BC=8,则sinA=( )A、
| ||
B、
| ||
C、
| ||
D、
|
在-2,0,-1,3这四个数中,最小的数是( )
| A、-2 | B、0 | C、-1 | D、3 |
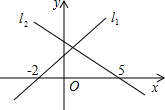 如图,在同一平面直角坐标系内,直线l1:y=kx+b与直线l2:y=mx+n分别与x轴交于点(-2,0)与(5,0),则不等式组
如图,在同一平面直角坐标系内,直线l1:y=kx+b与直线l2:y=mx+n分别与x轴交于点(-2,0)与(5,0),则不等式组
|
| A、x<-2 | B、x>5 |
| C、-2<x<5 | D、无解 |
 如图,菱形OABC的顶点O在坐标原点,OA在x轴正半轴上,菱形的边长为6,∠AOC=60°.动点P以每秒1个单位长度的速度从点O出发沿x轴正半轴的线路运动,动点Q以相同的速度从点C同时出发沿线路CB-BA运动.当点Q到达点A后,两点同时停止运动.在运动过程中,设动点P运动的时间为t(n),△CPQ的面积为S.
如图,菱形OABC的顶点O在坐标原点,OA在x轴正半轴上,菱形的边长为6,∠AOC=60°.动点P以每秒1个单位长度的速度从点O出发沿x轴正半轴的线路运动,动点Q以相同的速度从点C同时出发沿线路CB-BA运动.当点Q到达点A后,两点同时停止运动.在运动过程中,设动点P运动的时间为t(n),△CPQ的面积为S. 如图,AB为⊙O的弦,若OA⊥OD且BD=CD.
如图,AB为⊙O的弦,若OA⊥OD且BD=CD. 如图,A、C、F、B在同一直线上,AE=BD,EF=CD,AC=BF.求证:∠A=∠B.
如图,A、C、F、B在同一直线上,AE=BD,EF=CD,AC=BF.求证:∠A=∠B.