题目内容
某商场以每个30元的价格购进7000个计算器.物价部门规定:销售价格应在每个30元到70元之间(包括30元与70元).市场调研发现:单价定在70元时,日均可销售60个,单价每降低1元时,日均可多销售2个.在销售过程中,每天还要支付出其他费用500元(不足1天按1天算).设销售价为x元,日均获利为y元.
(1)求y与x之间的涵数关系式,并写出x的取值范围;
(2)单价定为多少元时,日均获利最多?最多是多少元;
(3)若将这批计算机全部售完,比较日均获利最多和销售单价最高这两种销售方式,哪一种获总利比较多,多出多少元?
(1)求y与x之间的涵数关系式,并写出x的取值范围;
(2)单价定为多少元时,日均获利最多?最多是多少元;
(3)若将这批计算机全部售完,比较日均获利最多和销售单价最高这两种销售方式,哪一种获总利比较多,多出多少元?
考点:二次函数的应用
专题:
分析:(1)由日均获利y=(售价-成本)×销售量-其他费用500元,由此关系式列出函数关系式;
(2)由(1)中的关系式配方,求最大值;
(3)分别计算出日均获利最多时的利润额和销售单价最高时的利润额,做差比较即可.
(2)由(1)中的关系式配方,求最大值;
(3)分别计算出日均获利最多时的利润额和销售单价最高时的利润额,做差比较即可.
解答:解:(1)由题意,得
y=(x-30)[60+2×(70-x)]-500,
=-2x2+260x-6500(30≤x≤70);
(2)y=-2x2+260x-6500=-2(x-65)2+1950.
当单价定为65元时,日均获利最多,是1950元;
(3)当日均获利最多时:
单价为65元,日均销售为:60+2×(70-65)=70kg,
那么获利为:1950×(7000÷70)=195000元.
当销售单价最高时单价为70元,
日均销售60kg,将这种化工原料全部售完需7000÷60≈117天,
那么获利为(70-30)×7000-117×500=221500元.
因为221500>195000,且221500-195000=26500元,
所以,销售单价最高时获利更多,且多获利26500元.
y=(x-30)[60+2×(70-x)]-500,
=-2x2+260x-6500(30≤x≤70);
(2)y=-2x2+260x-6500=-2(x-65)2+1950.
当单价定为65元时,日均获利最多,是1950元;
(3)当日均获利最多时:
单价为65元,日均销售为:60+2×(70-65)=70kg,
那么获利为:1950×(7000÷70)=195000元.
当销售单价最高时单价为70元,
日均销售60kg,将这种化工原料全部售完需7000÷60≈117天,
那么获利为(70-30)×7000-117×500=221500元.
因为221500>195000,且221500-195000=26500元,
所以,销售单价最高时获利更多,且多获利26500元.
点评:此题考查的是用二次函数解决实际问题.注意利用二次函数求最值时,关键是应用二次函数的性质:即由函数y随x的变化,结合自变量的取值范围确定最值.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
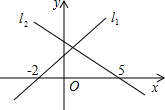 如图,在同一平面直角坐标系内,直线l1:y=kx+b与直线l2:y=mx+n分别与x轴交于点(-2,0)与(5,0),则不等式组
如图,在同一平面直角坐标系内,直线l1:y=kx+b与直线l2:y=mx+n分别与x轴交于点(-2,0)与(5,0),则不等式组
|
| A、x<-2 | B、x>5 |
| C、-2<x<5 | D、无解 |
 如图,AB为⊙O的弦,若OA⊥OD且BD=CD.
如图,AB为⊙O的弦,若OA⊥OD且BD=CD. 如图,A、C、F、B在同一直线上,AE=BD,EF=CD,AC=BF.求证:∠A=∠B.
如图,A、C、F、B在同一直线上,AE=BD,EF=CD,AC=BF.求证:∠A=∠B. 如图,在矩形ABCD中,AB=6,AD=10,O是BD上一点,以O为圆心作圆与AB相切于点G,
如图,在矩形ABCD中,AB=6,AD=10,O是BD上一点,以O为圆心作圆与AB相切于点G, 在学校舞蹈比赛中,10名学生参赛成绩统计如图,极差和中位数分别是
在学校舞蹈比赛中,10名学生参赛成绩统计如图,极差和中位数分别是