题目内容
 如图,菱形ABCD和菱形ECGF的边长分别为2和3,∠A=120°,则图中阴影部分的面积是
如图,菱形ABCD和菱形ECGF的边长分别为2和3,∠A=120°,则图中阴影部分的面积是考点:菱形的性质,相似三角形的判定与性质
专题:
分析:设BF与CE相交于点H,利用△BCH和△BGF相似,根据相似三角形对应边成比例列式求出CH,再求出DH,然后求出AB、GF之间的距离,再根据三角形的面积公式列式计算即可得解.
解答: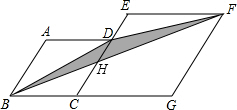 解:如图,设BF与CE相交于点H,
解:如图,设BF与CE相交于点H,
∵CE∥GF,
∴△BCH∽△BGF,
∴
=
,
即
=
,
解得CH=
,
∴DH=CD-CH=2-
=
,
∵∠A=120°,
∴AB、GF之间的距离=(2+3)×
=
,
∴阴影部分的面积=
×
×
=
.
故答案为:
.
 解:如图,设BF与CE相交于点H,
解:如图,设BF与CE相交于点H,∵CE∥GF,
∴△BCH∽△BGF,
∴
| CH |
| GF |
| BC |
| BG |
即
| CH |
| 3 |
| 2 |
| 2+3 |
解得CH=
| 6 |
| 5 |
∴DH=CD-CH=2-
| 6 |
| 5 |
| 4 |
| 5 |
∵∠A=120°,
∴AB、GF之间的距离=(2+3)×
| ||
| 2 |
5
| ||
| 2 |
∴阴影部分的面积=
| 1 |
| 2 |
| 4 |
| 5 |
5
| ||
| 2 |
| 3 |
故答案为:
| 3 |
点评:本题考查了菱形的性质,相似三角形的判定与性质,观察图形把阴影部分的面积分成等底的两个三角形求解是解题的关键.

练习册系列答案
相关题目
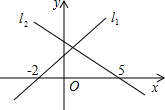 如图,在同一平面直角坐标系内,直线l1:y=kx+b与直线l2:y=mx+n分别与x轴交于点(-2,0)与(5,0),则不等式组
如图,在同一平面直角坐标系内,直线l1:y=kx+b与直线l2:y=mx+n分别与x轴交于点(-2,0)与(5,0),则不等式组
|
| A、x<-2 | B、x>5 |
| C、-2<x<5 | D、无解 |
 如图,半径为3的扇形OAB的面积为2π,则⊙O的圆周角∠ACB=
如图,半径为3的扇形OAB的面积为2π,则⊙O的圆周角∠ACB=