题目内容
15．在两个不透明的口袋中分别装有三个颜色分别为红色、白色、绿色的小球，这三个小球除颜色外其余都相同，若分别从两个口袋中随机取出一个小球，则取出的两个小球颜色相同的概率是$\frac{1}{3}$．分析 列表得出所有的情况个数，再找出颜色相同的情况个数，即可求出所求的概率．
解答 解：
根据题意列表如下：
| 红 | 白 | 绿 | |
| 红 | （红，红） | （白，红） | （绿，红） |
| 白 | （红，白） | （白，白） | （绿，白） |
| 绿 | （红，绿） | （白，绿） | （绿，绿） |
则P颜色相同=$\frac{3}{9}$=$\frac{1}{3}$．
故答案为：$\frac{1}{3}$．
点评 此题考查了列表法与树状图法，以及概率公式，用到的知识点为：概率=所求情况数与总情况数之比．
练习册系列答案
相关题目
3．圆柱的侧面展开图不可能是（ ）
| A． | 平行四边形 | B． | 正方形 | C． | 矩形 | D． | 梯形 |
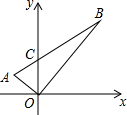如图，在直角坐标平面上，△AOB是直角三角形，点O在原点上，A、B两点的坐标分别为（-1，y1）、（3，y2），线段AB交y轴于点C．若S△AOC=1，记∠AOC为α，∠BOC为β，则sinα•sinβ的值为$\frac{3}{8}$．
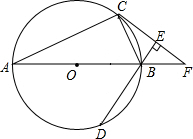如图，AB为⊙O的直径，C、D为⊙O上不同于A、B的两点，∠ABD=2∠BAC，过点C作CE⊥DB，垂足为点E，直线AB与CE交于点F．
如图，抛物线y=-x2+bx+c与直线AB相交于A（-1，0）、B（2，3）两点，与y轴交于点C，其顶点为D．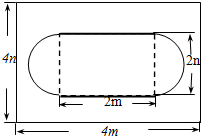
某居民小区为了美化环境，如图在一块长为4m，宽为4n的长方形绿地上建造花坛，花坛是由一个矩形和两个半圆组成的．求改造后剩下的绿地面积（π取3）．