题目内容
5.计算:(1)|$\sqrt{3}$-2|+(-$\frac{1}{3}$)-1-(2016-π)0+2cos30°
(2)先化简,再求值:($\frac{x-1}{x}$-$\frac{x-2}{x+1}$)÷$\frac{2{x}^{2}-x}{{x}^{2}+2x+1}$,其中x=-2.
分析 (1)分别根据0指数幂及负整数指数幂的计算法则、绝对值的性质、特殊角的三角函数值分别计算出各数,再根据实数混合运算的法则进行计算即可;
(2)先根据分式混合运算的法则把原式进行化简,再把x的值代入进行计算即可.
解答 解:(1)原式=2-$\sqrt{3}$-3-1+2×$\frac{\sqrt{3}}{2}$
=-$\sqrt{3}$-2+$\sqrt{3}$
=-2;
(2)原式=$\frac{{x}^{2}-1-{x}^{2}+2x}{x(x+1)}$•$\frac{{(x+1)}^{2}}{x(2x-1)}$
=$\frac{2x-1}{x(x+1)}$•$\frac{{(x+1)}^{2}}{x(2x-1)}$
=$\frac{x+1}{{x}^{2}}$,
当x=-2时,原式=$\frac{-2+1}{4}$=-$\frac{1}{4}$.
点评 本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.

练习册系列答案
 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
20. 如图,在平行四边形ABCD中,E是CD延长线上一点,BE与AD交于F,若CD=2DE,则$\frac{{S}_{△DEF}}{{S}_{△ABF}}$等于( )
如图,在平行四边形ABCD中,E是CD延长线上一点,BE与AD交于F,若CD=2DE,则$\frac{{S}_{△DEF}}{{S}_{△ABF}}$等于( )
 如图,在平行四边形ABCD中,E是CD延长线上一点,BE与AD交于F,若CD=2DE,则$\frac{{S}_{△DEF}}{{S}_{△ABF}}$等于( )
如图,在平行四边形ABCD中,E是CD延长线上一点,BE与AD交于F,若CD=2DE,则$\frac{{S}_{△DEF}}{{S}_{△ABF}}$等于( )| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{8}$ |
20.将分别标有数字0,1,2,3的司长卡片背面朝上洗匀后,抽取一张作为十位上的数字,再抽取一张作为个位上的数字,每次抽取都不放回,则所得的两位数恰好是奇数的概率等于( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{4}{9}$ | D. | $\frac{5}{9}$ |
10. 如图,在Rt△AOB中,OA=OB=5$\sqrt{2}$,⊙O的半径为3,点P是AB边上的动点,过点P作⊙O的一条切线PQ(点Q为切点),则切线PQ的最小值为( )
如图,在Rt△AOB中,OA=OB=5$\sqrt{2}$,⊙O的半径为3,点P是AB边上的动点,过点P作⊙O的一条切线PQ(点Q为切点),则切线PQ的最小值为( )
 如图,在Rt△AOB中,OA=OB=5$\sqrt{2}$,⊙O的半径为3,点P是AB边上的动点,过点P作⊙O的一条切线PQ(点Q为切点),则切线PQ的最小值为( )
如图,在Rt△AOB中,OA=OB=5$\sqrt{2}$,⊙O的半径为3,点P是AB边上的动点,过点P作⊙O的一条切线PQ(点Q为切点),则切线PQ的最小值为( )| A. | 3 | B. | 5$\sqrt{2}$-3 | C. | 4 | D. | 5 |
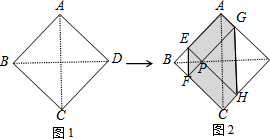 如图1,正方形纸片ABCD边长为2,折叠∠B和∠D,使两个直角的顶点重合于对角线BD上的一点P,EF、GH分别是折痕(图2).设AE=x(0<x<2),给出下列判断:
如图1,正方形纸片ABCD边长为2,折叠∠B和∠D,使两个直角的顶点重合于对角线BD上的一点P,EF、GH分别是折痕(图2).设AE=x(0<x<2),给出下列判断: