题目内容
15. 如图,一艘海轮位于灯塔P的北偏西80°方向的A处,它以每小时45海里的速度向正南方向航行,2小时后到达位于灯塔P的南偏西20°的B处,则B处与灯塔P的距离为( )
如图,一艘海轮位于灯塔P的北偏西80°方向的A处,它以每小时45海里的速度向正南方向航行,2小时后到达位于灯塔P的南偏西20°的B处,则B处与灯塔P的距离为( )| A. | 45海里 | B. | 60海里 | C. | 70海里 | D. | 90海里 |
分析 根据平行线的性质可以得出∠ABP=20°,根据角的运算即可得出∠BAP=80°=∠APB,从而得出BP=AB,再根据“路程=速度×时间”即可得出结论.
解答 解:在图中标上字母,如图所示.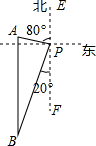
∵海轮从点A往正南方向航行,
∴AB∥EF,
∴∠ABP=∠BPF=20°.
∵∠APB=180°-∠APE-∠BPF=180°-80°-20°=80°,
∴∠BAP=180°-∠ABP-∠APB=80°,
∴BP=AB=45×2=/0(海里).
故选D.
点评 本题考查了等腰三角形的判定以及平行线的性质,解题的关键是找出△ABP为等腰三角形.本题属于基础题,难度不大,解该题型题目时,根据平行线的性质找出相等的角是关键.

练习册系列答案
相关题目
5.下列计算错误的是( )
| A. | a5+a5=2a5 | B. | (-2a2)3=-26 | C. | 2a2•a-1=2a | D. | $\root{3}{-27}$=-3 |
6.已知一直角三角形的两直角边长分别是6cm和8cm,则斜边上的中线长( )
| A. | 10 | B. | 3 | C. | 4 | D. | 5 |
7. 如图,AB是⊙O的直径,CD是⊙O的弦,∠ABD=57°,则∠C等于( )
如图,AB是⊙O的直径,CD是⊙O的弦,∠ABD=57°,则∠C等于( )
 如图,AB是⊙O的直径,CD是⊙O的弦,∠ABD=57°,则∠C等于( )
如图,AB是⊙O的直径,CD是⊙O的弦,∠ABD=57°,则∠C等于( )| A. | 53° | B. | 23° | C. | 57° | D. | 33° |
5.下列式子与$\sqrt{2}$是同类二次根式的是( )
| A. | $\sqrt{12}$ | B. | $\sqrt{0.2}$ | C. | $\sqrt{\frac{1}{2}}$ | D. | $\sqrt{28}$ |
