题目内容
11.已知a2-3a+1=0,(a≠0).求代数式a4+$\frac{1}{{a}^{4}}$的值.分析 已知等式两边除以a变形后,两边平方求出a2+$\frac{1}{{a}^{2}}$的值,再两边平方即可求出所求式子的值.
解答 解:已知等式变形得:a+$\frac{1}{a}$=3,
两边平方得:(a+$\frac{1}{a}$)2=a2+$\frac{1}{{a}^{2}}$+2=9,即a2+$\frac{1}{{a}^{2}}$=7,
两边平方得:(a2+$\frac{1}{{a}^{2}}$)2=a4+$\frac{1}{{a}^{4}}$+2=49,
则a4+$\frac{1}{{a}^{4}}$=47.
点评 本题考查了分式的混合运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
 在一次暖气管道的铺设工程中,由点A出发沿正西方向进行,在点A的南偏西55°的方向上有一个敬老院B,占地是以B为中心方圆100m的圆,当工程进行了200m后到达C处,此时B在C南偏西25°的方向上.请你根据题中所提供的信息计算并分析一下,工程继续进行下去,是否会穿越敬老院.
在一次暖气管道的铺设工程中,由点A出发沿正西方向进行,在点A的南偏西55°的方向上有一个敬老院B,占地是以B为中心方圆100m的圆,当工程进行了200m后到达C处,此时B在C南偏西25°的方向上.请你根据题中所提供的信息计算并分析一下,工程继续进行下去,是否会穿越敬老院.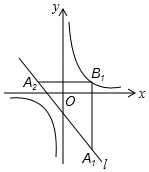 如图,在平面直角坐标系中,已知直线l:y=-x-1,双曲线y=$\frac{1}{x}$.在直线l上取点A1,过点A1作x轴的垂线交双曲线于点B1,过点B1作y轴的垂线交直线l于点A2,继续操作:过点A2作x轴的垂线交双曲线于点B2,过点B2作y轴的垂线交直线l于点A3,…,依次这样得到双曲线上的点B1,B2,B3,B4,…,Bn.记点A1的横坐标为2,则B2016的坐标为(-$\frac{1}{3}$,-3).
如图,在平面直角坐标系中,已知直线l:y=-x-1,双曲线y=$\frac{1}{x}$.在直线l上取点A1,过点A1作x轴的垂线交双曲线于点B1,过点B1作y轴的垂线交直线l于点A2,继续操作:过点A2作x轴的垂线交双曲线于点B2,过点B2作y轴的垂线交直线l于点A3,…,依次这样得到双曲线上的点B1,B2,B3,B4,…,Bn.记点A1的横坐标为2,则B2016的坐标为(-$\frac{1}{3}$,-3).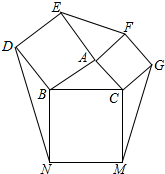 如图,以△ABC的边AB、AC、BC为一边,分别向三角形的外侧作正方形ABDE,正方形ACGF、正方形BCMN
如图,以△ABC的边AB、AC、BC为一边,分别向三角形的外侧作正方形ABDE,正方形ACGF、正方形BCMN