题目内容
6．先化简（a-1-$\frac{1}{a-1}$）÷$\frac{{a}^{2}-4a+4}{a-1}$，再从不等式a＜2a+1的解集中选一个合适的值代入求值．分析 根据分式的混合运算法则先化简，后取一个使得式子有意义的数代入即可（注意a≠1或2）．
解答 解：原式=$\frac{（a-1）^{2}-1}{a-1}$•$\frac{a-1}{（a-2）^{2}}$
=$\frac{a（a-2）}{a-1}$•$\frac{a-1}{（a-2）^{2}}$
=$\frac{a}{a-2}$，
∵a＜2a+1
∴-a＜1，
∴a＞-1，
当a=0时，原式=0．
点评 本题考查分式的混合运算法则、代数式求值问题等知识，正确通过、约分是解题的关键，属于中考常考题型．
练习册系列答案
相关题目
16．
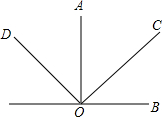如图，OA⊥OB，OC⊥OD，∠AOC=α，那么∠B0D等于（ ）
如图，OA⊥OB，OC⊥OD，∠AOC=α，那么∠B0D等于（ ）| A． | 180°-2α | B． | 180°-α | C． | 90°+$\frac{1}{2}$α | D． | 2α-90° |
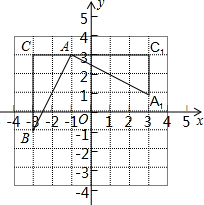如图，在平面直角坐标系中，A（-1，3），B（-3，-1），C（-3，3），已知△A1AC1是由△ABC旋转得到的．
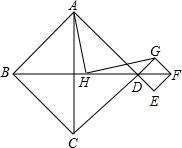四边形ABCD与四边形DEFG都是正方形，点H为BF的中点，连接HA，HG．若三点B、D、F在同一直线上，如图探索HA与HG的数量及位置关系，并予以证明．