题目内容
2．D、E、F分别是△ABC三边的中点，L、M、N分别是△DEF三边的中点，若△ABC的周长为16cm，则△LMN的周长是4cm．分析 根据三角形的中位线平行于第三边并且等于第三边的一半可知中点三角形的周长等于原三角形的周长的一半，然后解答即可．
解答 解：∵D、E、F为△ABC的三边中点，
∴△DEF的周长=$\frac{1}{2}$×△ABC的周长=$\frac{1}{2}$×16=8cm，
∵L、M、N分别是△DEF三边的中点，
∴△LMN的周长=$\frac{1}{2}$×△DEF的周长=$\frac{1}{2}$×8=4cm．
故答案为：4．
点评 本题考查了三角形的中位线定理，熟记定理以及中点三角形的周长与原三角形的关系是解题的关键．
练习册系列答案
智能训练练测考系列答案
相关题目
12．
如图所示，如果△AOB与△AOD的周长之差为8，而AB：AD=3：2，那么?ABCD的周长（ ）
如图所示，如果△AOB与△AOD的周长之差为8，而AB：AD=3：2，那么?ABCD的周长（ ）| A． | 16 | B． | 24 | C． | 40 | D． | 80 |
13．填表：
| 抛物线 | 开口方向 | 对称轴 | 顶点坐标 |
| y=x2-4x+1 | 向上 | x=2 | （2，-3） |
| y=-5（x+2）（x-4） | 向下 | x=1 | （1，45） |
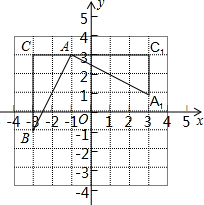如图，在平面直角坐标系中，A（-1，3），B（-3，-1），C（-3，3），已知△A1AC1是由△ABC旋转得到的．