题目内容
6.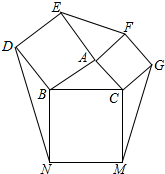 如图,以△ABC的边AB、AC、BC为一边,分别向三角形的外侧作正方形ABDE,正方形ACGF、正方形BCMN
如图,以△ABC的边AB、AC、BC为一边,分别向三角形的外侧作正方形ABDE,正方形ACGF、正方形BCMN(1)以EF、DN、GM为边能否构成三角形?为什么?
(2)若能,试探究以EF、DN、GM为边构成的三角形的面积与△ABC的面积的关系.
分析 (1)可以利用正方形的对边平行而且相等,作出一个以EF、GM、ND为边的三角形,把△AEF沿AB平移,△MCG沿CB方向平移,使A、C重合于B,F、G重合于I,△DBI≌△AEF,△BIN≌△MCG,且可得∠EAF+∠GCM+∠DBN=360°,因此可拼成一个三角形;
(2)然后再证明S△DIN=3S△ABC,把△GCM绕C点旋转90°,得到△BCG′,可得A,C,G′在一条直线上,且C为AG′的中点.进而由DN、EF、GM为三边构成的△DIK的面积S△DIN=3S△ABC.
解答 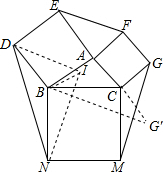 证明:(1)以EF、DN、GM为边能构成三角形,
证明:(1)以EF、DN、GM为边能构成三角形,
理由:把△AEF沿AB平移,△MCG沿CB方向平移,
使A、C重合于B,F、G重合于I,连接DI,BI,NI,
∴△DBI≌△AEF,△BIN≌△MCG,
∴∠EAF+∠GCM+∠DBN=360°,DI=EF,IN=GM,
∵DI,IN,DN为边能拼成一个△DIK,
∴以EF、DN、GM为边能拼成一个△DIK;
(2)把△GCM绕C点旋转90°,得到△BCG′,
∵∠ACG=90°,
∴∠ACG+∠GCG′=180°,
∴A,C,G′在一条直线上,CG′=CG=AC,
∴C为AG′的中点,
∴S△BCG′=S△ABC,
∴S△BIN=S△ABC,同理S△DBN=S△DBI=S△ABC,
∴DN、EF、GM为三边构成的△DIN的面积S△DIN=3S△ABC.
点评 本题主要考查对三角形的三边关系定理,全等三角形的性质和判定,三角形的面积等知识点的理解和掌握,综合运用这些性质进行推理是解此题的关键.

练习册系列答案
 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案 小题狂做系列答案
小题狂做系列答案
相关题目
18.如果a表示一个负数,则|a|等于( )
| A. | a | B. | 0 | C. | -a | D. | 不确定 |
 如图,已知△ABC和△ADE是等边三角形,联结BD、CE.
如图,已知△ABC和△ADE是等边三角形,联结BD、CE.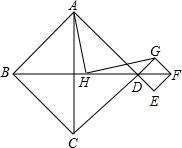 四边形ABCD与四边形DEFG都是正方形,点H为BF的中点,连接HA,HG.若三点B、D、F在同一直线上,如图探索HA与HG的数量及位置关系,并予以证明.
四边形ABCD与四边形DEFG都是正方形,点H为BF的中点,连接HA,HG.若三点B、D、F在同一直线上,如图探索HA与HG的数量及位置关系,并予以证明.
 如图,平面直角坐标系xOy中点A的坐标为(-1,1),点B的坐标为(3,3),抛物线经过A、O、B三点,连接OA、OB、AB,线段AB交y轴于点E.
如图,平面直角坐标系xOy中点A的坐标为(-1,1),点B的坐标为(3,3),抛物线经过A、O、B三点,连接OA、OB、AB,线段AB交y轴于点E.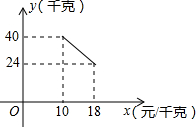 某经销商销售一种产品,这种产品的成本价为10元/千克,已知销售价不低于成本价,且物价部门规定这种产品的销售价不高于18元/千克,市场调查发现,该产品每天的销售量y(千克)与销售价x(元/千克)之间的函数关系如图所示:
某经销商销售一种产品,这种产品的成本价为10元/千克,已知销售价不低于成本价,且物价部门规定这种产品的销售价不高于18元/千克,市场调查发现,该产品每天的销售量y(千克)与销售价x(元/千克)之间的函数关系如图所示: