题目内容
1. 在一次暖气管道的铺设工程中,由点A出发沿正西方向进行,在点A的南偏西55°的方向上有一个敬老院B,占地是以B为中心方圆100m的圆,当工程进行了200m后到达C处,此时B在C南偏西25°的方向上.请你根据题中所提供的信息计算并分析一下,工程继续进行下去,是否会穿越敬老院.
在一次暖气管道的铺设工程中,由点A出发沿正西方向进行,在点A的南偏西55°的方向上有一个敬老院B,占地是以B为中心方圆100m的圆,当工程进行了200m后到达C处,此时B在C南偏西25°的方向上.请你根据题中所提供的信息计算并分析一下,工程继续进行下去,是否会穿越敬老院.(利用以下数据进行计算:tan25°≈0.47,tan35°≈0.70,tan55°≈1.43,tan65°≈2.14.)
分析 作BD⊥AC于D,设BD为xm,根据正切的概念分别求出AD、CD,列式计算求出BD,比较即可.
解答 解: 作BD⊥AC于D,
作BD⊥AC于D,
设BD为xm,
由题意得,∠ABD=55°,∠DBC=25°,
则AD=BD•tan∠ABD=1.43x,
CD=BD•tan∠DBC=0.47x,
由题意得,1.43x-0.47x=200,
解得,x≈208m,
208m>100m,
答:工程继续进行下去,不会穿越敬老院.
点评 此题主要考查的是解直角三角形-方向角问题,求三角形的边或高的问题一般可以转化为解直角三角形的问题,解决的方法就是作高线.

练习册系列答案
 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
12. 如图所示,如果△AOB与△AOD的周长之差为8,而AB:AD=3:2,那么?ABCD的周长( )
如图所示,如果△AOB与△AOD的周长之差为8,而AB:AD=3:2,那么?ABCD的周长( )
 如图所示,如果△AOB与△AOD的周长之差为8,而AB:AD=3:2,那么?ABCD的周长( )
如图所示,如果△AOB与△AOD的周长之差为8,而AB:AD=3:2,那么?ABCD的周长( )| A. | 16 | B. | 24 | C. | 40 | D. | 80 |
16.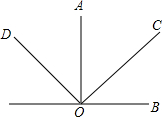 如图,OA⊥OB,OC⊥OD,∠AOC=α,那么∠B0D等于( )
如图,OA⊥OB,OC⊥OD,∠AOC=α,那么∠B0D等于( )
 如图,OA⊥OB,OC⊥OD,∠AOC=α,那么∠B0D等于( )
如图,OA⊥OB,OC⊥OD,∠AOC=α,那么∠B0D等于( )| A. | 180°-2α | B. | 180°-α | C. | 90°+$\frac{1}{2}$α | D. | 2α-90° |
13.填表:
| 抛物线 | 开口方向 | 对称轴 | 顶点坐标 |
| y=x2-4x+1 | 向上 | x=2 | (2,-3) |
| y=-5(x+2)(x-4) | 向下 | x=1 | (1,45) |
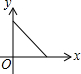
 如图,在一条笔直的小路上有一盏路灯,晚上小雷从点B处径直走到点A处时,小雷在灯光照射下的影长y与行走的路程x之间的函数图象大致是( )
如图,在一条笔直的小路上有一盏路灯,晚上小雷从点B处径直走到点A处时,小雷在灯光照射下的影长y与行走的路程x之间的函数图象大致是( )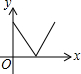
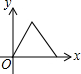
 如图,已知AB∥CD,且$\frac{{S}_{△ABE}}{{S}_{△ADE}}$=$\frac{2}{3}$,求$\frac{{S}_{△ABE}}{{S}_{△DCE}}$的值.
如图,已知AB∥CD,且$\frac{{S}_{△ABE}}{{S}_{△ADE}}$=$\frac{2}{3}$,求$\frac{{S}_{△ABE}}{{S}_{△DCE}}$的值.