题目内容
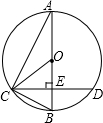 如图,已知AB为⊙O的直径,CD是弦,且AB⊥CD于点E.连接AC、OC、BC.
如图,已知AB为⊙O的直径,CD是弦,且AB⊥CD于点E.连接AC、OC、BC.(1)图中与∠A相等的角有
(2)若EB=8cm,CD=24cm,求⊙O的直径.
考点:垂径定理,勾股定理
专题:
分析:(1)由AB为⊙O的直径,CD是弦,且AB⊥CD,由垂径定理即可求得
=
,然后由圆周角定理,可得∠BCD=∠A,又由等腰三角形的性质,即可得∠ACO=∠;
(2)首先设半径为xcm,即可得x2=122+(x-8)2,继而求得答案.
 |
| BC |
 |
| BD |
(2)首先设半径为xcm,即可得x2=122+(x-8)2,继而求得答案.
解答:解:(1)∵AB为⊙O的直径,CD是弦,且AB⊥CD,
∴
=
,
∴∠BCD=∠A,
∵OA=OC,
∴∠ACO=∠A,
∴与∠A相等的角有:∠BCD,∠ACO.
故答案为:∠BCD,∠ACO;
(2)设⊙O的半径为xcm,则OC=xcm,OE=OB-BE=x-8(cm),
∵AB⊥CD,CD=24cm,
∴CE=
CD=12cm,
在Rt△OCE中,OC2=OE2+CE2,
∴x2=122+(x-8)2,
解得:x=13,
∴⊙O的直径为26cm.
∴
 |
| BC |
 |
| BD |
∴∠BCD=∠A,
∵OA=OC,
∴∠ACO=∠A,
∴与∠A相等的角有:∠BCD,∠ACO.
故答案为:∠BCD,∠ACO;
(2)设⊙O的半径为xcm,则OC=xcm,OE=OB-BE=x-8(cm),
∵AB⊥CD,CD=24cm,
∴CE=
| 1 |
| 2 |
在Rt△OCE中,OC2=OE2+CE2,
∴x2=122+(x-8)2,
解得:x=13,
∴⊙O的直径为26cm.
点评:此题考查了垂径定理、圆周角定理以及勾股定理.此题难度不大,注意掌握数形结合思想与方程思想的应用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目




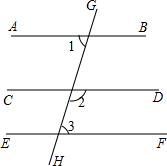 如图,直线AB、CD、EF被直线GH所截,∠1=70°,∠2=110°,∠2+∠3=180°,试说明:(1)EF∥AB.(2)CD∥AB( 补全横线及括号的内容 )
如图,直线AB、CD、EF被直线GH所截,∠1=70°,∠2=110°,∠2+∠3=180°,试说明:(1)EF∥AB.(2)CD∥AB( 补全横线及括号的内容 ) 如图,DE∥BC,CG=GB,∠1=∠2,求证:△DGE是等腰三角形.
如图,DE∥BC,CG=GB,∠1=∠2,求证:△DGE是等腰三角形.