题目内容
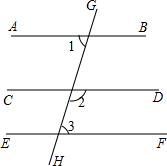 如图,直线AB、CD、EF被直线GH所截,∠1=70°,∠2=110°,∠2+∠3=180°,试说明:(1)EF∥AB.(2)CD∥AB( 补全横线及括号的内容 )
如图,直线AB、CD、EF被直线GH所截,∠1=70°,∠2=110°,∠2+∠3=180°,试说明:(1)EF∥AB.(2)CD∥AB( 补全横线及括号的内容 )证明:(1)∵∠2+∠3=180°,∠2=110°(已知 )
∴∠3=70°
又∵∠1=70°(已知 )
∴∠1=∠3
∴EF∥AB
(2)∵∠2+∠3=180°
∴
又∵EF∥AB ( 已证 )
∴
考点:平行线的判定
专题:推理填空题
分析:(1)先将∠2=110°代入∠2+∠3=180°,求出∠3=70°,根据等量代换得到∠1=∠3,由内错角相等,两直线平行即可证明EF∥AB;
(2)先由同旁内角互补,两直线平行得出CD∥EF,再根据两条直线都和第三条直线平行,那么这两条直线平行即可证明CD∥AB.
(2)先由同旁内角互补,两直线平行得出CD∥EF,再根据两条直线都和第三条直线平行,那么这两条直线平行即可证明CD∥AB.
解答:证明:(1)∵∠2+∠3=180°,∠2=110°(已知 ),
∴∠3=70°(等量代换),
又∵∠1=70°(已知 ),
∴∠1=∠3(等量代换),
∴EF∥AB(内错角相等,两直线平行);
(2)∵∠2+∠3=180°,
∴CD∥EF(同旁内角互补,两直线平行),
又∵EF∥AB ( 已证 ),
∴CD∥AB(两条直线都和第三条直线平行,那么这两条直线平行).
故答案为等量代换,等量代换,内错角相等,两直线平行;CD,EF,CD,AB.
∴∠3=70°(等量代换),
又∵∠1=70°(已知 ),
∴∠1=∠3(等量代换),
∴EF∥AB(内错角相等,两直线平行);
(2)∵∠2+∠3=180°,
∴CD∥EF(同旁内角互补,两直线平行),
又∵EF∥AB ( 已证 ),
∴CD∥AB(两条直线都和第三条直线平行,那么这两条直线平行).
故答案为等量代换,等量代换,内错角相等,两直线平行;CD,EF,CD,AB.
点评:本题考查了平行线的判定:同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补,两直线平行;两条直线都和第三条直线平行,那么这两条直线平行.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
下列各点在直线y=2x+6上的是( )
| A、(-5,-4) | ||||
| B、(-7,20) | ||||
C、(-
| ||||
D、(
|
如果多项式x2+mx+9是一个完全平方式,则m的值是( )
| A、±3 | B、3 | C、±6 | D、6 |
晚上小亮在路灯下散步,在小亮从远处走到灯下,再远离路灯这一过程中,他在地上的影子( )
| A、逐渐变短 |
| B、先变短后变长 |
| C、先变长后变短 |
| D、逐渐变长 |
 如图,已知:?ABCD中,CE⊥AD,CF⊥AB,∠B=50°,求∠ECF的度数.
如图,已知:?ABCD中,CE⊥AD,CF⊥AB,∠B=50°,求∠ECF的度数.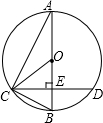 如图,已知AB为⊙O的直径,CD是弦,且AB⊥CD于点E.连接AC、OC、BC.
如图,已知AB为⊙O的直径,CD是弦,且AB⊥CD于点E.连接AC、OC、BC.