题目内容
为了方便广大游客到昆明参观游览,铁路部门临时增开了一列南宁-昆明的直达快车,已知南宁-昆明两地相距900千米,一列普快列车与一列直达快车都由南宁开往昆明,直达快车的平均速度是普快车速度的1.5倍,直达快车比普快车晚发1小时,比普快车早2小时到达昆明,求两车的平均速度.
考点:分式方程的应用
专题:
分析:有路程900千米,求的是速度,那么一定是根据时间来列等量关系的.关键描述语是:“直达快车比普快车晚发1小时,比普快车早2小时到达昆明”.等量关系为:普通快车用的时间=直达快车用的时间+1+2.
解答:解:设普通快车的平均速度为每小时x千米,则直达快车的平均速度为每小时1.5x千米.
依题意得
=
+1+2,
解得,x=100,
经检验,x=100是原方程的根.
则1.5x=150.
答:普通快车的平均速度为每小时100千米,直达快车的平均速度为每小时150千米.
依题意得
| 900 |
| x |
| 900 |
| 1.5x |
解得,x=100,
经检验,x=100是原方程的根.
则1.5x=150.
答:普通快车的平均速度为每小时100千米,直达快车的平均速度为每小时150千米.
点评:此题主要考查了分式方程的应用,应用题中一般有三个量,求一个量,明显的有一个量,一定是根据另一量来列等量关系的.本题考查分式方程的应用,分析题意,找到关键描述语,找到合适的等量关系是解决问题的关键.

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
如果多项式x2+mx+9是一个完全平方式,则m的值是( )
| A、±3 | B、3 | C、±6 | D、6 |
 一条笔直的公路上有A、B、C三地,B、C两地相距150千米,甲、乙两辆汽车分别以B、C两地同时出发,沿公路匀速相向而行,分别驶往C、B 两地.甲、乙两车到A地的距离y1、y2(千米)与行驶时间x(时)的关系如图.下列结论:
一条笔直的公路上有A、B、C三地,B、C两地相距150千米,甲、乙两辆汽车分别以B、C两地同时出发,沿公路匀速相向而行,分别驶往C、B 两地.甲、乙两车到A地的距离y1、y2(千米)与行驶时间x(时)的关系如图.下列结论: 如图,已知:?ABCD中,CE⊥AD,CF⊥AB,∠B=50°,求∠ECF的度数.
如图,已知:?ABCD中,CE⊥AD,CF⊥AB,∠B=50°,求∠ECF的度数.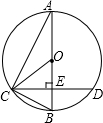 如图,已知AB为⊙O的直径,CD是弦,且AB⊥CD于点E.连接AC、OC、BC.
如图,已知AB为⊙O的直径,CD是弦,且AB⊥CD于点E.连接AC、OC、BC.