题目内容
△ABC中,AB=AC,D是BC边上一点,连接AD,E为△ABC外一点,连接DE、AE和BE,AD=DE,BE∥AC.
(1)如图1,求证:∠BED=∠DAB.
(2)如图2,当D为BC中点时,作DF⊥AC于F,连接BF交DE于点H,作AK⊥BF分别交BF、DF于点G、K,AF=4DK,试探究线段DH和AE之间的数量关系,并证明你的结论.

(1)如图1,求证:∠BED=∠DAB.
(2)如图2,当D为BC中点时,作DF⊥AC于F,连接BF交DE于点H,作AK⊥BF分别交BF、DF于点G、K,AF=4DK,试探究线段DH和AE之间的数量关系,并证明你的结论.

考点:相似形综合题
专题:
分析:(1)过点D作DM⊥AB于M,过点D作DN⊥EB于N,根据AB=AC,得出∠1=∠C,再根据AC∥BE,得出∠2=∠C,从而得出∠2=∠1,即DM=DN,在Rt△ADM和Rt△EDN中,根据HL得出△ADM≌△EDN,即可得出∠BED=∠DAB;
(2)根据AB=AC,BD=DC,得出AD⊥BC,根据AA得出△ADK∽△BCF,从而得出tan∠ACB=
=
=
,即可得出K为DF中点,延长ED交AC延长线于P,作DO∥FC交BF于O,设DK=a,得出AF、DF、AD的值,再根据∠FDC=∠DAF,得出FC=a,再根据AAS得出△EBD≌△PCD,从而得出DE=AD=DP,再根据DF⊥AC,得出AF=FP,AD=DP,AE=2DF,CP的值,最后根据DO∥FC,得出
=
=
,求出DH的值即可.
(2)根据AB=AC,BD=DC,得出AD⊥BC,根据AA得出△ADK∽△BCF,从而得出tan∠ACB=
| DF |
| CF |
| AD |
| DC |
| AD | ||
|
| PF |
| DO |
| HP |
| DH |
DH+2
| ||
| DH |
解答:解: (1)过点D作DM⊥AB于M,过点D作DN⊥EB于N,
(1)过点D作DM⊥AB于M,过点D作DN⊥EB于N,
∵AB=AC,
∴∠1=∠C,
∵AC∥BE,
∴∠2=∠C,
∴∠2=∠1,
∴DM=DN,
在Rt△ADM和Rt△EDN中,
,
∴△ADM≌△EDN,
∴∠BED=∠DAB;
(2)DH=
AE;
证明:
∵AB=AC,BD=DC,
∴AD⊥BC,
∵∠AGB=∠ADB=90°,∠3=∠4,
∴∠KAD=∠FBC,
∵∠ACB+∠FDC=90°,∠ADF+∠FDC=90°,
∴∠ACB=∠ADF,
∴△ADK∽△BCF,
∴
=
,
∵tan∠ACB=
=
=
,
∴DK=
DF,
∴K为DF中点,
延长ED交AC延长线于P,作DO∥FC交BF于O,设DK=a,
∴AF=4a,DF=2a,AD=2
a,
∵∠FDC=∠DAF,
∴
=
,
∴FC=a,
∵DO∥FC,
∴DQ=
CF=
a,
∵
,
∴△EBD≌△PCD,
∴DE=AD=DP,
∵DF⊥AC,
∴AF=FP=4a,AD=DP=2
a,AE=2DF=4a,CP=3a,
∵DO∥FC,
∴
=
=
,
∴DH=
a,
∴DH=
AE.
 (1)过点D作DM⊥AB于M,过点D作DN⊥EB于N,
(1)过点D作DM⊥AB于M,过点D作DN⊥EB于N,∵AB=AC,
∴∠1=∠C,
∵AC∥BE,
∴∠2=∠C,
∴∠2=∠1,
∴DM=DN,
在Rt△ADM和Rt△EDN中,
|
∴△ADM≌△EDN,
∴∠BED=∠DAB;
(2)DH=
| ||
| 14 |
证明:
∵AB=AC,BD=DC,
∴AD⊥BC,
∵∠AGB=∠ADB=90°,∠3=∠4,
∴∠KAD=∠FBC,
∵∠ACB+∠FDC=90°,∠ADF+∠FDC=90°,
∴∠ACB=∠ADF,
∴△ADK∽△BCF,
∴
| DK |
| CF |
| AD |
| BC |
∵tan∠ACB=
| DF |
| CF |
| AD |
| DC |
| AD | ||
|
∴DK=
| 1 |
| 2 |
∴K为DF中点,
延长ED交AC延长线于P,作DO∥FC交BF于O,设DK=a,

∴AF=4a,DF=2a,AD=2
| 5 |
∵∠FDC=∠DAF,
∴
| FC |
| DF |
| DF |
| AF |
∴FC=a,
∵DO∥FC,
∴DQ=
| 1 |
| 2 |
| 1 |
| 2 |
∵
|
∴△EBD≌△PCD,
∴DE=AD=DP,
∵DF⊥AC,
∴AF=FP=4a,AD=DP=2
| 5 |
∵DO∥FC,
∴
| PF |
| DO |
| HP |
| DH |
DH+2
| ||
| DH |
∴DH=
2
| ||
| 7 |
∴DH=
| ||
| 14 |
点评:此题考查了相似形综合,用到的知识点是全等三角形和相似三角形的判定与性质、平行线的性质、特殊角的三角函数值等,关键是根据题意做出辅助线,构造直角三角形,运用数形结合思想解答.

练习册系列答案
相关题目
下列计算正确的是( )
| A、a4+a4=a8 |
| B、-(-m2)3=m5 |
| C、x4•x4=x16 |
| D、(-xy2)3=-x3y6 |
 如图,在平面直角坐标系中,矩形纸片ABCD的顶点坐标是A(0,0),C(6,4),E(5,0).将矩形纸片沿直线l折叠,设A′是点A落在矩形CD边上的对应点,点A′的横坐标为2.直线l与x轴、y轴的交点分别为E、F.
如图,在平面直角坐标系中,矩形纸片ABCD的顶点坐标是A(0,0),C(6,4),E(5,0).将矩形纸片沿直线l折叠,设A′是点A落在矩形CD边上的对应点,点A′的横坐标为2.直线l与x轴、y轴的交点分别为E、F. 如图,在坐标系中,菱形ABCD的边BC与x轴重合,点B与原点重合,AB=10,∠ABC=60°.动点P从点B出发沿BC边以每秒1个单位长的速度匀速运动;动点Q从点D出发沿折线DC-CB-BA以每秒3个单位长的速度匀速运动,过点P作PF⊥BC,交折线AB-AC于点E,交直线AD于点F.若P、Q两点同时出发,当其中一点到达终点时整个运动随之停止,设运动时间为t秒.
如图,在坐标系中,菱形ABCD的边BC与x轴重合,点B与原点重合,AB=10,∠ABC=60°.动点P从点B出发沿BC边以每秒1个单位长的速度匀速运动;动点Q从点D出发沿折线DC-CB-BA以每秒3个单位长的速度匀速运动,过点P作PF⊥BC,交折线AB-AC于点E,交直线AD于点F.若P、Q两点同时出发,当其中一点到达终点时整个运动随之停止,设运动时间为t秒.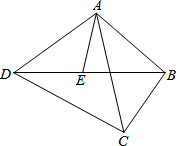 已知:如图,点E是四边形ABCD的对角线BD上一点,且∠BAC=∠BDC=∠DAE.
已知:如图,点E是四边形ABCD的对角线BD上一点,且∠BAC=∠BDC=∠DAE.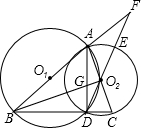 如图,点O2是⊙O1上一点,⊙O2与⊙O1相交于A、D两点,BC⊥AD于D,分别交⊙O1、⊙O2于B、C两点,延长DO2交⊙O2于E,交BA的延长线于F,BO2交AD于G,连AC.
如图,点O2是⊙O1上一点,⊙O2与⊙O1相交于A、D两点,BC⊥AD于D,分别交⊙O1、⊙O2于B、C两点,延长DO2交⊙O2于E,交BA的延长线于F,BO2交AD于G,连AC.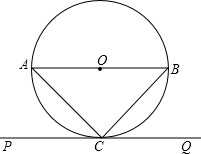 如图,线段AB是圆O的直径,直线PQ经过圆上一点C,PQ∥AB,连结AC、BC,且AC=BC,AC=5
如图,线段AB是圆O的直径,直线PQ经过圆上一点C,PQ∥AB,连结AC、BC,且AC=BC,AC=5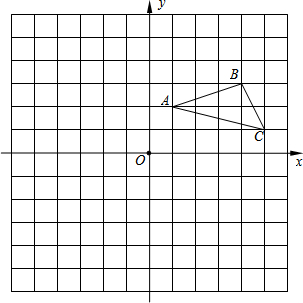 在平面直角坐标系中,△ABC的位置如图,网格中小正方形的边长为1,请解答下列问题:
在平面直角坐标系中,△ABC的位置如图,网格中小正方形的边长为1,请解答下列问题: