题目内容
1. 如图,在△ABC中,∠C=90°,∠A=30°,BD是∠ABC的平分线.若AB=6,则点D到AB的距离是$\sqrt{3}$.
如图,在△ABC中,∠C=90°,∠A=30°,BD是∠ABC的平分线.若AB=6,则点D到AB的距离是$\sqrt{3}$.
分析 求出∠ABC,求出∠DBC,根据含30度角的直角三角形性质求出BC,CD,问题即可求出.
解答 解:∵∠C=90°,∠A=30°,
∴∠ABC=180°-30°-90°=60°,
∵BD是∠ABC的平分线,
∴∠DBC=$\frac{1}{2}$∠ABC=30°,
∴BC=$\frac{1}{2}$AB=3,
∴CD=BC•tan30°=3×$\frac{\sqrt{3}}{3}$=$\sqrt{3}$,
∵BD是∠ABC的平分线,
又∵角平线上点到角两边距离相等,
∴点D到AB的距离=CD=$\sqrt{3}$,
故答案为:$\sqrt{3}$.
点评 本题考查了角平分线上的点到角的两边的距离相等的性质,熟记性质是解题的关键.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
12.等腰三角形边长分别为a,b,2,且a,b是关于x的一元二次方程x2-6x+n-1=0的两根,则n的值为
( )
( )
| A. | 9 | B. | 10 | C. | 9或10 | D. | 8或10 |
16.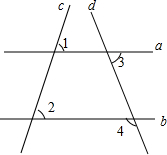 直线a、b、c、d的位置如图所示,如果∠1=58°,∠2=58°,∠3=70°,那么∠4等于( )
直线a、b、c、d的位置如图所示,如果∠1=58°,∠2=58°,∠3=70°,那么∠4等于( )
 直线a、b、c、d的位置如图所示,如果∠1=58°,∠2=58°,∠3=70°,那么∠4等于( )
直线a、b、c、d的位置如图所示,如果∠1=58°,∠2=58°,∠3=70°,那么∠4等于( )| A. | 58° | B. | 70° | C. | 110° | D. | 116° |
6.若∠A=34°,则∠A的补角为( )
| A. | 56° | B. | 146° | C. | 156° | D. | 166° |