题目内容
11.已知一次函数y=kx+b的图象经过两点A(0,1),B(2,0),则当x≥2时,y≤0.分析 利用待定系数法把点A(0,-1),B(1,0)代入y=kx+b,可得关于k、b的方程组,再解出方程组可得k、b的值,进而得到函数解析式,再解不等式即可.
解答 解:∵一次函数y=kx+b的图象经过两点A(0,1),B(2,0),
∴$\left\{\begin{array}{l}{b=1}\\{2k+b=0}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-\frac{1}{2}}\\{b=1}\end{array}\right.$
这个一次函数的表达式为y=-$\frac{1}{2}$x+1.
解不等式-$\frac{1}{2}$x+1≤0,
解得x≥2.
故答案为x≥2.
点评 本题考查了待定系数法求一次函数解析式,解不等式,把点的坐标代入函数解析式求出解析式是解题的关键.

练习册系列答案
 百年学典课时学练测系列答案
百年学典课时学练测系列答案 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案
相关题目
2.下列实数中,是无理数的为( )
| A. | $\sqrt{3}$ | B. | $\frac{1}{3}$ | C. | 0 | D. | -3 |
6.若不等式组$\left\{\begin{array}{l}{x<1}\\{x>m-1}\end{array}\right.$恰有两个整数解,则m的取值范围是( )
| A. | -1≤m<0 | B. | -1<m≤0 | C. | -1≤m≤0 | D. | -1<m<0 |
3.某班开展1分钟仰卧起坐比赛活动,5名同学的成绩如下(单位:个):37、38、40、40、42.这组数据的众数是( )
| A. | 37 | B. | 38 | C. | 40 | D. | 42 |
20.下列计算正确的是( )
| A. | a2+a2=2a4 | B. | 2a2×a3=2a6 | C. | 3a-2a=1 | D. | (a2)3=a6 |
1.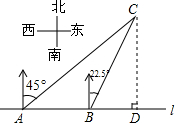 如图,在一笔直的海岸线l上有A、B两个观测站,AB=2km、从A测得船C在北偏东45°的方向,从B测得船C在北偏东22.5°的方向,则船C离海岸线l的距离(即CD的长)为( )
如图,在一笔直的海岸线l上有A、B两个观测站,AB=2km、从A测得船C在北偏东45°的方向,从B测得船C在北偏东22.5°的方向,则船C离海岸线l的距离(即CD的长)为( )
 如图,在一笔直的海岸线l上有A、B两个观测站,AB=2km、从A测得船C在北偏东45°的方向,从B测得船C在北偏东22.5°的方向,则船C离海岸线l的距离(即CD的长)为( )
如图,在一笔直的海岸线l上有A、B两个观测站,AB=2km、从A测得船C在北偏东45°的方向,从B测得船C在北偏东22.5°的方向,则船C离海岸线l的距离(即CD的长)为( )| A. | 4km | B. | (2+$\sqrt{2}$)km | C. | 2$\sqrt{2}$km | D. | (4-$\sqrt{2}$)km |
 如图,在△ABC中,∠C=90°,∠A=30°,BD是∠ABC的平分线.若AB=6,则点D到AB的距离是$\sqrt{3}$.
如图,在△ABC中,∠C=90°,∠A=30°,BD是∠ABC的平分线.若AB=6,则点D到AB的距离是$\sqrt{3}$.