题目内容
9.(1)计算:|-5|+$\sqrt{4}$×2-1;(2)化简:a(2-a)+(a+1)(a-1).
分析 (1)首先求出-5的绝对值,然后根据整式的混合运算顺序,计算乘法和加法,求出算式|-5|+$\sqrt{4}$×2-1的值是多少即可.
(2)根据整式的混合运算顺序,首先计算乘法和,然后计算加法,求出算式a(2-a)+(a+1)(a-1)的值是多少即可.
解答 解:(1)|-5|+$\sqrt{4}$×2-1;
=5+2×$\frac{1}{2}$
=5+1
=6
(2)a(2-a)+(a+1)(a-1)
=2a-a2+a2-1
=2a-1
点评 (1)此题主要考查了整式的混合运算,要熟练掌握,解答此题的关键是要明确:有乘方、乘除的混合运算中,要按照先乘方后乘除的顺序运算,其运算顺序和有理数的混合运算顺序相似.
(2)此题还考查了负整数指数幂的运算,要熟练掌握,解答此题的关键是要明确:①a-p=$\frac{1}{{a}^{p}}$(a≠0,p为正整数);②计算负整数指数幂时,一定要根据负整数指数幂的意义计算;③当底数是分数时,只要把分子、分母颠倒,负指数就可变为正指数.
(3)此题还考查了绝对值的非负性,以及算术平方根的求法,要熟练掌握.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案
相关题目
20. 如图,已知点A,B,C,D,E,F是边长为1的正六边形的顶点,连接任意两点均可得到一条线段.在连接两点所得的所有线段中任取一条线段,取到长度为$\sqrt{3}$的线段的概率为( )
如图,已知点A,B,C,D,E,F是边长为1的正六边形的顶点,连接任意两点均可得到一条线段.在连接两点所得的所有线段中任取一条线段,取到长度为$\sqrt{3}$的线段的概率为( )
 如图,已知点A,B,C,D,E,F是边长为1的正六边形的顶点,连接任意两点均可得到一条线段.在连接两点所得的所有线段中任取一条线段,取到长度为$\sqrt{3}$的线段的概率为( )
如图,已知点A,B,C,D,E,F是边长为1的正六边形的顶点,连接任意两点均可得到一条线段.在连接两点所得的所有线段中任取一条线段,取到长度为$\sqrt{3}$的线段的概率为( )| A. | $\frac{1}{4}$ | B. | $\frac{2}{5}$ | C. | $\frac{2}{3}$ | D. | $\frac{5}{9}$ |
17.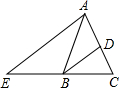 如图,在△ABC中,AB=AC,BD平分∠ABC交AC于点D,AE∥BD交CB的延长线于点E.若∠E=35°,则∠BAC的度数为( )
如图,在△ABC中,AB=AC,BD平分∠ABC交AC于点D,AE∥BD交CB的延长线于点E.若∠E=35°,则∠BAC的度数为( )
 如图,在△ABC中,AB=AC,BD平分∠ABC交AC于点D,AE∥BD交CB的延长线于点E.若∠E=35°,则∠BAC的度数为( )
如图,在△ABC中,AB=AC,BD平分∠ABC交AC于点D,AE∥BD交CB的延长线于点E.若∠E=35°,则∠BAC的度数为( )| A. | 40° | B. | 45° | C. | 60° | D. | 70° |
 如图,抛物线与x轴交于点A(-$\frac{1}{3}$,0)、点B(2,0),与y轴交于点C(0,1),连接BC.
如图,抛物线与x轴交于点A(-$\frac{1}{3}$,0)、点B(2,0),与y轴交于点C(0,1),连接BC.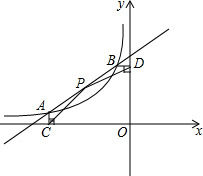 如图,A(-4,$\frac{1}{2}$),B(-1,2)是一次函数y1=ax+b与反比例函数y2=$\frac{m}{x}$图象的两个交点,AC⊥x轴于点C,BD⊥y轴于点D.
如图,A(-4,$\frac{1}{2}$),B(-1,2)是一次函数y1=ax+b与反比例函数y2=$\frac{m}{x}$图象的两个交点,AC⊥x轴于点C,BD⊥y轴于点D. 如图,在△ABC中,∠C=90°,∠A=30°,BD是∠ABC的平分线.若AB=6,则点D到AB的距离是$\sqrt{3}$.
如图,在△ABC中,∠C=90°,∠A=30°,BD是∠ABC的平分线.若AB=6,则点D到AB的距离是$\sqrt{3}$. 如图,已知在△ABC中,∠A=90°
如图,已知在△ABC中,∠A=90°