题目内容
13.关于x的方程kx2-4x-$\frac{2}{3}$=0有实数根,则k的取值范围是k≥-6.分析 由于k的取值不确定,故应分k=0(此时方程化简为一元一次方程)和k≠0(此时方程为二元一次方程)两种情况进行解答.
解答 解:当k=0时,-4x-$\frac{2}{3}$=0,解得x=-$\frac{1}{6}$,
当k≠0时,方程kx2-4x-$\frac{2}{3}$=0是一元二次方程,
根据题意可得:△=16-4k×(-$\frac{2}{3}$)≥0,
解得k≥-6,k≠0,
综上k≥-6,
故答案为k≥-6.
点评 本题考查的是根的判别式,注意掌握一元二次方程ax2+bx+c=0(a≠0)的根与△=b2-4ac有如下关系:①当△>0时,方程有两个不相等的两个实数根;②当△=0时,方程有两个相等的两个实数根;③当△<0时,方程无实数根.同时解答此题时要注意分k=0和k≠0两种情况进行讨论.

练习册系列答案
相关题目
3.如果三角形三条边的中垂线的交点在三角形的外部,那么,这个三角形是( )
| A. | 直角三角形 | B. | 锐角三角形 | C. | 钝角三角形 | D. | 等边三角形 |
5.在|-2|,20,2-1,$\sqrt{2}$这四个数中,最大的数是( )
| A. | |-2| | B. | 20 | C. | 2-1 | D. | $\sqrt{2}$ |
2.下列实数中,是无理数的为( )
| A. | $\sqrt{3}$ | B. | $\frac{1}{3}$ | C. | 0 | D. | -3 |
3.某班开展1分钟仰卧起坐比赛活动,5名同学的成绩如下(单位:个):37、38、40、40、42.这组数据的众数是( )
| A. | 37 | B. | 38 | C. | 40 | D. | 42 |
 如图,抛物线与x轴交于点A(-$\frac{1}{3}$,0)、点B(2,0),与y轴交于点C(0,1),连接BC.
如图,抛物线与x轴交于点A(-$\frac{1}{3}$,0)、点B(2,0),与y轴交于点C(0,1),连接BC. 如图,在△ABC中,∠C=90°,∠A=30°,BD是∠ABC的平分线.若AB=6,则点D到AB的距离是$\sqrt{3}$.
如图,在△ABC中,∠C=90°,∠A=30°,BD是∠ABC的平分线.若AB=6,则点D到AB的距离是$\sqrt{3}$. 如图是由6个相同的小正方体搭成的几何体,那么这个几何体的俯视图是( )
如图是由6个相同的小正方体搭成的几何体,那么这个几何体的俯视图是( )



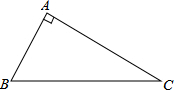 如图,已知在△ABC中,∠A=90°
如图,已知在△ABC中,∠A=90°