题目内容
14.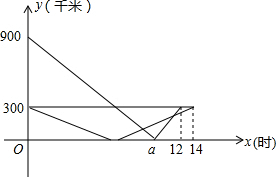 甲、乙两车在连通A、B、C三地的公路上行驶,甲车从A地出发匀速向C地行驶,同时乙车从C地出发匀速向B地行驶,到达B地并在B地停留2小时后,按原路原速返回到C地.在两车行驶的过程中,甲、乙两车距B地的路程y(千米)与行驶时间x(小时)之间的函数图象如图所示,请结合图象回答下列问题:
甲、乙两车在连通A、B、C三地的公路上行驶,甲车从A地出发匀速向C地行驶,同时乙车从C地出发匀速向B地行驶,到达B地并在B地停留2小时后,按原路原速返回到C地.在两车行驶的过程中,甲、乙两车距B地的路程y(千米)与行驶时间x(小时)之间的函数图象如图所示,请结合图象回答下列问题:(1)求a的值;
(2)求乙车从B地返回到C地的过程中,y与x之间的函数关系式;
(3)求当甲、乙两车第一次行驶到距B地的路程相等时y的值.
分析 (1)由已知图象求出甲、乙的速度.
(2)根据图象上的点先求出乙车从B地返回到C地的函数解析式,
(3)再由设甲车从A地到B地的函数解析式是y1=k1x+b1,和甲车从B地到C地的函数解析式是y2=k2x+b2,由已知求出解析式结合(2)求出的解析式求解.
解答  解:(1)由已知图象得:甲的速度为:(900+300)÷12=100km/h,乙的速度为(300+300)÷(14-2)=50km/h,
解:(1)由已知图象得:甲的速度为:(900+300)÷12=100km/h,乙的速度为(300+300)÷(14-2)=50km/h,
∵甲的速度为:100km/h,与B地相距900km,
∴时间=$\frac{900}{100}$=9,
∴a的值是9;
(2)设乙车从B地返回到C地的函数解析式是y=kx+b,
∵乙的速度为(300+300)÷(14-2)=50km/h,
∴乙到B地的时间是300÷50=6(小时),
6+2=8,
即点M(8,0),如图,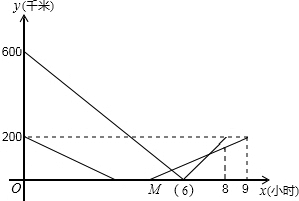
∵图象经过M(8,0),(14,300)两点.
∴8k+b=0,14k+b=300
解得:$\left\{\begin{array}{l}{k=50}\\{b=-400}\end{array}\right.$,
∴y=50x-400,
答:乙车从B地返回到C地的过程中,y与x之间的函数关系式为y=50x-400(8≤x≤14);
(3)设甲车从A地到B地的函数解析式是y1=k1x+b1,
∵图象经过(0,900),(8,0)两点,
∴$\left\{\begin{array}{l}{900={b}_{1}}\\{0=8{k}_{1}+{b}_{1}}\end{array}\right.$,解得:$\left\{\begin{array}{l}{k=-112.5}\\{b=900}\end{array}\right.$,
∴y1=-112.5x+900,
设甲车从B地到C地的函数解析式是y2=k2x+b2,
∵图象经过(12,300),(8,0)两点,
∴$\left\{\begin{array}{l}{0=8{k}_{2}+{b}_{2}}\\{300=12{k}_{2}+{b}_{2}}\end{array}\right.$,解得:$\left\{\begin{array}{l}{{k}_{2}=75}\\{{b}_{2}=-600}\end{array}\right.$,
∴y2=75x-600,
由$\left\{\begin{array}{l}{y=50x-400}\\{{y}_{1}=-112.5x+900}\end{array}\right.$和$\left\{\begin{array}{l}{y=50x-400}\\{{y}_{2}=75x-600}\end{array}\right.$,
解得:y=0(千米)或y=0(千米).
答:当甲、乙两车行驶到距B地的路程相等时,甲、乙两车距B地的路程是0千米.
点评 此题考查的知识点是一次函数的应用,关键是根据图象先求出甲、乙的速度.

 阅读快车系列答案
阅读快车系列答案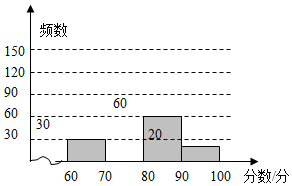 为了庆祝即将到来的2017年元旦,某校举行了书法比赛,赛后整理参赛同学的成绩,并制作成图表如下:
为了庆祝即将到来的2017年元旦,某校举行了书法比赛,赛后整理参赛同学的成绩,并制作成图表如下:| 分数段 | 频数 | 频率 |
| 60≤x<70 | 30 | 0.15 |
| 70≤x<80 | m | 0.45 |
| 80≤x<90 | 60 | n |
| 90≤x≤100 | 20 | 0.1 |
(1)这次共调查了200名学生;表中的数m=90,n=0.3;
(2)请在图中补全频数分布直方图;
(3)若绘制扇形统计图,分数段60≤x<70所对应扇形的圆心角的度数是54°;
(4)如果比赛成绩在80分以上(含80分)可获得奖励,那么获奖概率是多少?
| x | … | -4 | -3 | -2 | -1 | 0 | … |
| y | … | 3 | -2 | -5 | -6 | -5 | … |
| A. | 抛物线开口向下 | |
| B. | 抛物线与y轴交于正半轴 | |
| C. | 方程ax2+bx+c=0的正根在1与2之间 | |
| D. | 当x=-3时的函数值比x=1.5时的函数值大 |
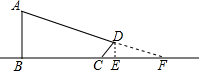 小明在某一时刻测得1m的杆子在阳光下的影子长为2m,他想测量电线杆AB的高度,但其影子恰好落在土坡的坡面CD和地面BC上,量得CD=4m,BC=10m,CD与底面成45°,求电线杆的高度.
小明在某一时刻测得1m的杆子在阳光下的影子长为2m,他想测量电线杆AB的高度,但其影子恰好落在土坡的坡面CD和地面BC上,量得CD=4m,BC=10m,CD与底面成45°,求电线杆的高度. 已知抛物线y=x2-2x-a.
已知抛物线y=x2-2x-a.