题目内容
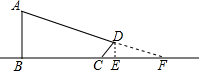
4．
如图，O是坐标原点，菱形OABC的顶点B的坐标为（0，4），反比例函数y=-$\frac{8}{x}$（x＜0）的图象经过点A，则菱形OABC的面积为16．
分析 过点A作AD⊥OB于点D，根据反比例函数系数k的几何意义得出△AOD的面积，再由菱形的性质即可得出结论．
解答 
解：过点A作AD⊥OB于点D，
∵函数y=-$\frac{8}{x}$（x＜0）的图象经过点A，
∴S△AOD=4．
∵四边形OABC是菱形，
∴S菱形OABC=4S△AOD=16．
故答案为：16．
点评 本题考查的是反比例函数系数k的几何意义，熟知在反比例函数y=$\frac{k}{x}$的图象上任意一点向坐标轴作垂线，这一点和垂足以及坐标原点所构成的三角形的面积是$\frac{1}{2}$|k|，且保持不变是解答此题的关键．
练习册系列答案
阅读快车系列答案
相关题目
12．某房地产开发公司计划建A、B两种户型的住房共80套，A种户型每套成本和售价分别为90万元和102万元，B种户型每套成本和售价分别为60万元和70万元．设计划建A户型x套，所建户型全部售出后获得的总利润为W万元．
【思考】
（1）根据所给条件，完成下表：
（2）求W与x之间的函数解析式；
【探究】
（3）该公司所建房资金不少于5700万元，且所筹资金全部用于建房，若A户型不超过32套，则该公司有哪几种建房方案？
（4）在（3）的前提下，根据国家房地产政策，公司计划每套A户型住房的售价降低a万元（0＜a≤3），B户型住房的售价不变，且预计所建的两种住房全部售出，求该公司获得最大利润的方案．
【决策】
为了适应市场需要，该公司在总套数不变的情况下，改建若干套C户型，现已知C户型每套成本110万元，售价118万元．若该公司所筹资金为6300万元且刚好用完，则当x=45套时，该公司所建房售出后获得的总利润最大．
【思考】
（1）根据所给条件，完成下表：
| A户型 | B户型 | |
| 套数 | x | 80-x |
| 利润（万元） | 12x | 10（80-x） |
【探究】
（3）该公司所建房资金不少于5700万元，且所筹资金全部用于建房，若A户型不超过32套，则该公司有哪几种建房方案？
（4）在（3）的前提下，根据国家房地产政策，公司计划每套A户型住房的售价降低a万元（0＜a≤3），B户型住房的售价不变，且预计所建的两种住房全部售出，求该公司获得最大利润的方案．
【决策】
为了适应市场需要，该公司在总套数不变的情况下，改建若干套C户型，现已知C户型每套成本110万元，售价118万元．若该公司所筹资金为6300万元且刚好用完，则当x=45套时，该公司所建房售出后获得的总利润最大．
19．若点A（a，-2）、B（4，b）在正比例函数y=kx的图象上，则下列等式一定成立的是（ ）
| A． | a-b=6 | B． | a+b=-10 | C． | a•b=-8 | D． | $\frac{a}{b}$=-2 |
小明在某一时刻测得1m的杆子在阳光下的影子长为2m，他想测量电线杆AB的高度，但其影子恰好落在土坡的坡面CD和地面BC上，量得CD=4m，BC=10m，CD与底面成45°，求电线杆的高度．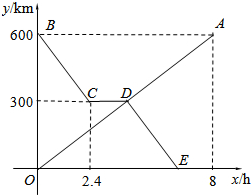
货车和轿车分别从甲、乙两地同时出发，沿同一公路相向而行．轿车出发3h后休息，直至与货车相遇后，以原速度继续行驶．设货车出发xh后，货车、轿车分别到达离甲地y1km和y2km的地方，图中的线段OA、折线BCDE分别表示y1、y2与x之间的函数关系．
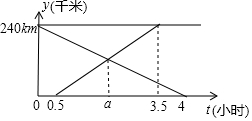甲、乙两车分别从A、B两地相向而行，甲车出发0.5小时后乙车出发，并以各自速度匀速行驶，两车相遇后依然按照原速度原方向各自行驶，如图所示是两车离B地距离y与甲车出发时间t（小时）之间的函数图象．