题目内容
15.若am=-2,an=-$\frac{1}{2}$,则a2m+3n=-$\frac{1}{2}$.分析 首先根据幂的乘方的运算方法,求出a2m、a3n的值各是多少;然后根据同底数幂的乘法法则:同底数幂相乘,底数不变,指数相加,求出a2m+3n的值是多少即可.
解答 解:∵am=-2,an=-$\frac{1}{2}$,
∴a2m=(am)2=(-2)2=4,a3n=(an)3=${(-\frac{1}{2})}^{3}$=-$\frac{1}{8}$,
∴a2m+3n=4×(-$\frac{1}{8}$)=-$\frac{1}{2}$.
故答案为:-$\frac{1}{2}$.
点评 (1)此题主要考查了同底数幂的乘法法则:同底数幂相乘,底数不变,指数相加,要熟练掌握,解答此题的关键是要明确:①底数必须相同;②按照运算性质,只有相乘时才是底数不变,指数相加.
(2)此题还考查了幂的乘方和积的乘方,要熟练掌握,解答此题的关键是要明确:①(am)n=amn(m,n是正整数);②(ab)n=anbn(n是正整数).

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4.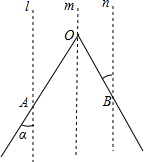 如图,已知:∠AOB=60°,点A、B分别在∠AOB两边上,直线l、m、n分别过A、O、B三点,且满足直线l∥m∥n,OB与直线n所夹的角为25°,则∠α的度数为( )
如图,已知:∠AOB=60°,点A、B分别在∠AOB两边上,直线l、m、n分别过A、O、B三点,且满足直线l∥m∥n,OB与直线n所夹的角为25°,则∠α的度数为( )
 如图,已知:∠AOB=60°,点A、B分别在∠AOB两边上,直线l、m、n分别过A、O、B三点,且满足直线l∥m∥n,OB与直线n所夹的角为25°,则∠α的度数为( )
如图,已知:∠AOB=60°,点A、B分别在∠AOB两边上,直线l、m、n分别过A、O、B三点,且满足直线l∥m∥n,OB与直线n所夹的角为25°,则∠α的度数为( )| A. | 25° | B. | 45° | C. | 35° | D. | 30° |
5.下列选项是无理数的为( )
| A. | $-\frac{1}{3}$ | B. | $\sqrt{4}$ | C. | 3.1 | D. | -π |
