题目内容
5.已知实数m,n,p,q满足m+n=p+q=4,mp+nq=6,则(m2+n2)pq+mn(p2+q2)=60.分析 先利用单项式乘以多项式法则将要求值的多项式进行整理,将题目所给的有确定值的式子进行变形,得出所需要的式子的值,运用整体代入法既可求解.
解答 解:∵m+n=p+q=4
∴(m+n)(p+q)=4×4=16
∵(m+n)(p+q)=mp+mq+np+nq
∴mp+mq+np+nq=16
∵mp+nq=6
∴mq+np=10
∴(m2+n2)pq+mn(p2+q2)
=m2pq+n2pq+mnp2+mnq2
=mp•mq+np•nq+mp•np+nq•mq
=mp•mq+mp•np+np•nq+nq•mq
=mp(mq+np)+np(nq+mq)
=(mp+nq)(np+mq)
=6×10
=60
故答案为60
点评 本题需要综合运用单项式乘以多项式、多项式乘以多项式法则,将式子通过变形后整体代入求解,解题的关键是对条件所给的式子变形要有方向性和目的性,同时要掌握分组分解法对式子进行因式分解,有一定难度.

练习册系列答案
相关题目
17.若数轴上表示数x的点在原点的左边,则化简|x|+$\sqrt{{x}^{2}}$的结果是( )
| A. | 2x | B. | -2x | C. | 0 | D. | x |
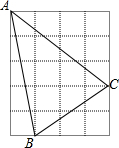 阅读:直角三角形具有下列性质,若直角三角形的两直角分别为a,b.斜边为c,则a2+b2=c2,利用这一性质.可求出某些线段的长,如图,正方形网格中,每个小正方形的边长均为1,则BC2=22+32,即BC=$\sqrt{2^2+3^2}$=$\sqrt{13}$,因3$<\sqrt{13}<$4,所以线段BC的长是无理数,请你利用以上阅读材料,判断图中线段AC、AB的长是有理数还是无理数,并说明理由.
阅读:直角三角形具有下列性质,若直角三角形的两直角分别为a,b.斜边为c,则a2+b2=c2,利用这一性质.可求出某些线段的长,如图,正方形网格中,每个小正方形的边长均为1,则BC2=22+32,即BC=$\sqrt{2^2+3^2}$=$\sqrt{13}$,因3$<\sqrt{13}<$4,所以线段BC的长是无理数,请你利用以上阅读材料,判断图中线段AC、AB的长是有理数还是无理数,并说明理由.