题目内容
17. 如图,Rt△ABC中,∠A=90°,D是BC的中点,E、F分别是AB、AC上的点,DE⊥DF.求证:EF2=BE2+CF2.(提示:要延长ED或FD,还要连接几条线段)
如图,Rt△ABC中,∠A=90°,D是BC的中点,E、F分别是AB、AC上的点,DE⊥DF.求证:EF2=BE2+CF2.(提示:要延长ED或FD,还要连接几条线段)
分析 延长FD到点G,使DG=DF,连接BG、EG,易证EF=EG,△CDF≌△BDG,可得BG=CF,∠DBG=∠C,即可求得∠ABG=90°,即可判定△BEG是直角三角形,根据勾股定理可得BE2+BG2=EG2,即可解题.
解答 证明:延长FD到点G,使DG=DF,连接BG、EG,如图所示: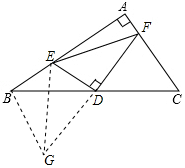
∵∠EDF=90°,DF=DG,
∴DE垂直平分FG,
∴EF=EG,
∵D是BC中点,
∴CD=BD,
在△CDF和△BDG中,$\left\{\begin{array}{l}{DF=DG}&{\;}\\{∠CDF=∠BDG}&{\;}\\{CD=BD}&{\;}\end{array}\right.$,
∴△CDF≌△BDG(SAS),
∴BG=CF,∠DBG=∠C,
∵∠A=90°,
∴∠C+∠ABC=90°,
∴∠ABG=∠ABC+∠DBG=90°,
∴△BEG是直角三角形,
∴BE2+BG2=EG2,
∴EF2=BE2+CF2.
点评 本题考查了全等三角形的判定,全等三角形对应边相等的性质以及直角三角形中勾股定理的运用,本题中求证△CDF≌△BDG是解题的关键.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
19.下列各题的结果正确的是( )
| A. | 3x+3y=6xy | B. | 16y2-7y2=9 | ||
| C. | -2(m-n)=-2m-2n | D. | 19a2b-9a2b=10a2b |
20.如果将抛物线y=x2+3向下平移1个单位,那么所得新抛物线的解析式是( )
| A. | y=(x-1)2+3 | B. | y=(x+1)2+3 | C. | y=x2+2 | D. | y=x2+4 |
5.一个圆柱的底面半径为Rcm,高为8cm,若它的高不变,将底面半径增加了2cm,体积相应增加了192πcm,则R=( )
| A. | 4cm | B. | 5cm | C. | 6cm | D. | 7cm |
12.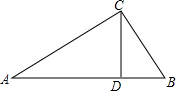 如图,在Rt△ABC中,∠C=90°,CD⊥AB,垂足为D,AD=4,DB=1,则CD的长为( )
如图,在Rt△ABC中,∠C=90°,CD⊥AB,垂足为D,AD=4,DB=1,则CD的长为( )
 如图,在Rt△ABC中,∠C=90°,CD⊥AB,垂足为D,AD=4,DB=1,则CD的长为( )
如图,在Rt△ABC中,∠C=90°,CD⊥AB,垂足为D,AD=4,DB=1,则CD的长为( )| A. | 2 | B. | $\sqrt{3}$ | C. | $\sqrt{5}$ | D. | $\sqrt{15}$ |
 如图,AD是∠BAC的平分线,DE⊥AB于E,DF⊥AC于F,且DB=DC,求证:BE=CF.
如图,AD是∠BAC的平分线,DE⊥AB于E,DF⊥AC于F,且DB=DC,求证:BE=CF.
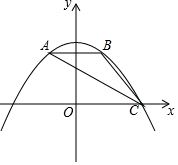 如图,抛物线y=ax2+$\frac{9}{4}$经过△ABC的三个顶点,点A坐标为(-1,2),点B是点A关于y轴的对称点,点C在x轴的正半轴上.
如图,抛物线y=ax2+$\frac{9}{4}$经过△ABC的三个顶点,点A坐标为(-1,2),点B是点A关于y轴的对称点,点C在x轴的正半轴上.