题目内容
12.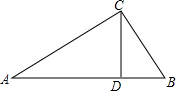 如图,在Rt△ABC中,∠C=90°,CD⊥AB,垂足为D,AD=4,DB=1,则CD的长为( )
如图,在Rt△ABC中,∠C=90°,CD⊥AB,垂足为D,AD=4,DB=1,则CD的长为( )| A. | 2 | B. | $\sqrt{3}$ | C. | $\sqrt{5}$ | D. | $\sqrt{15}$ |
分析 根据直角三角形的性质可以证明△ACD∽△CBD,然后根据相似三角形的对应边的比相等即可求解.
解答 解:∵在Rt△ABC中,∠C=90°,CD⊥AB,垂足为D,
∴∠ACD+∠BCD=90°,
∵∠BAC+∠ABC=90°,
∴∠ACD=∠ABC,
∵∠ADC=∠BDC=90°,
∴△ACD∽△CBD,
∴$\frac{AD}{CD}=\frac{CD}{DB}$,
即$\frac{1}{CD}=\frac{CD}{4}$,
解得:CD=2,
故选A.
点评 本题考查了相似三角形的判定与性质,理解△ACD∽△CBD是关键.

练习册系列答案
 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
14.下列方程是一元二次方程的是( )
| A. | x2-1=y | B. | (x+2)(x+1)=x2 | C. | 6x2=5 | D. | x+1=$\frac{1}{x}$ |
15.一种细菌的半径约为0.00004米,这个数用科学记数法表示为( )
| A. | 4×10-5 | B. | 0.4×10-6 | C. | 4×10-4 | D. | 40×10-4 |
7.1-6个月的婴儿生长发育得非常快,出生体重为4000克的婴儿,他们的体重y(克)和月龄x(月)之间的关系如表所示,则6个月大的婴儿的体重为( )
| 月龄/(月) | 1 | 2 | 3 | 4 | 5 |
| 体重/(克) | 4700 | 5400 | 6100 | 6800 | 7500 |
| A. | 7600克 | B. | 7800克 | C. | 8200克 | D. | 8500克 |
 如图,Rt△ABC中,∠A=90°,D是BC的中点,E、F分别是AB、AC上的点,DE⊥DF.求证:EF2=BE2+CF2.(提示:要延长ED或FD,还要连接几条线段)
如图,Rt△ABC中,∠A=90°,D是BC的中点,E、F分别是AB、AC上的点,DE⊥DF.求证:EF2=BE2+CF2.(提示:要延长ED或FD,还要连接几条线段)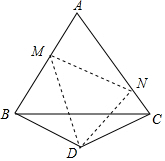 如图,△ABC是边长为10cm的等边三角形,△BDC是等腰三角形,且∠BDC=120°.以D为顶点作一个60°角,使其两边分别交AB于点M,交AC于点N,连接MN,则△AMN的周长为20.
如图,△ABC是边长为10cm的等边三角形,△BDC是等腰三角形,且∠BDC=120°.以D为顶点作一个60°角,使其两边分别交AB于点M,交AC于点N,连接MN,则△AMN的周长为20.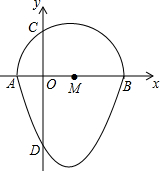 我们把一个半圆与抛物线的一部分组成的封闭图形称为“蛋圆”.如图,A、B、C、D分别是某蛋圆和坐标轴的交点其中抛物线的解析式为y=x2-2x-3,则“蛋圆”的弦CD的长为3+$\sqrt{3}$.
我们把一个半圆与抛物线的一部分组成的封闭图形称为“蛋圆”.如图,A、B、C、D分别是某蛋圆和坐标轴的交点其中抛物线的解析式为y=x2-2x-3,则“蛋圆”的弦CD的长为3+$\sqrt{3}$.