题目内容
20.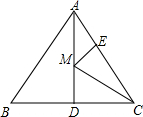 如图,等边△ABC的边长为6,AD是BC边上的中线,M是AD上的动点,E是AC边的中点,则EM+CM的最小值为3$\sqrt{3}$.
如图,等边△ABC的边长为6,AD是BC边上的中线,M是AD上的动点,E是AC边的中点,则EM+CM的最小值为3$\sqrt{3}$.
分析 先连接BM,再根据MB=MC,将EM+CM转化为EM+BM,最后根据两点之间线段最短,求得BE的长,即为EM+CM的最小值.
解答  解:连接BM,
解:连接BM,
∵等边△ABC中,AD是BC边上的中线
∴AD是BC边上的高线,即AD垂直平分BC
∴MB=MC
当B、M、E三点共线时,EM+CM=EM+BM=BE
∵等边△ABC中,E是AC边的中点
∴直角三角形ABE中,BE=$\sqrt{A{B}^{2}-A{E}^{2}}$=$\sqrt{{6}^{2}-{3}^{2}}$=$3\sqrt{3}$
∴EM+CM的最小值为$3\sqrt{3}$
故答案为:$3\sqrt{3}$
点评 本题主要考查了等边三角形的轴对称性质和勾股定理的应用等知识,熟练掌握和运用等边三角形的性质以及轴对称的性质是解决本题的关键.解题时注意,最小值问题一般需要考虑两点之间线段最短或垂线段最短等结论.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10. 如图,AB∥CD,点E在BC上,∠D=64°,∠DEB=108°,则∠B的度数为( )
如图,AB∥CD,点E在BC上,∠D=64°,∠DEB=108°,则∠B的度数为( )
 如图,AB∥CD,点E在BC上,∠D=64°,∠DEB=108°,则∠B的度数为( )
如图,AB∥CD,点E在BC上,∠D=64°,∠DEB=108°,则∠B的度数为( )| A. | 64° | B. | 44° | C. | 32° | D. | 54° |
15.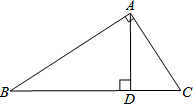 如图,在Rt△ABC中,∠BAC=90°,AD⊥BC于点D,则下列结论不正确的是( )
如图,在Rt△ABC中,∠BAC=90°,AD⊥BC于点D,则下列结论不正确的是( )
 如图,在Rt△ABC中,∠BAC=90°,AD⊥BC于点D,则下列结论不正确的是( )
如图,在Rt△ABC中,∠BAC=90°,AD⊥BC于点D,则下列结论不正确的是( )| A. | $sinB=\frac{AD}{AB}$ | B. | $sinB=\frac{AC}{BC}$ | C. | $sinB=\frac{AD}{AC}$ | D. | $sinB=\frac{CD}{AC}$ |
5.下列运算正确的是( )
| A. | 5x4-x2=4x2 | B. | 3a2•a3=3a6 | C. | (2a2)3(-ab)=-8a7b | D. | 2x2÷2x2=0 |
 如图,△ABC是边长为1的正三角形,弧AB和弧AC所对的圆心角均为120°,则图中阴影部分的面积为$\frac{\sqrt{3}}{12}$.
如图,△ABC是边长为1的正三角形,弧AB和弧AC所对的圆心角均为120°,则图中阴影部分的面积为$\frac{\sqrt{3}}{12}$.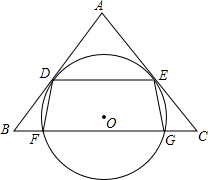 如图,O是△ABC内一点,⊙O与BC相交于F、G两点,且与AB、AC分别相切于点D、E,DE∥BC,连接DF、EG.
如图,O是△ABC内一点,⊙O与BC相交于F、G两点,且与AB、AC分别相切于点D、E,DE∥BC,连接DF、EG.