题目内容
11.在同一平面内,△ABC和△ABD如图①放置,其中AB=BD.小明做了如下操作:
将△ABC绕着边AC的中点旋转180°得到△CEA,将△ABD绕着边AD的中点旋转180°得到△DFA,如图②,请完成下列问题:
(1)试猜想四边形ABDF是什么特殊四边形,并说明理由;
(2)连接EF,CD,如图③,求证:四边形CDFE是平行四边形.
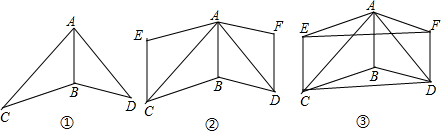
分析 (1)根旋转的性质得AB=DF,BD=FA,由于AB=BD,所以AB=BD=DF=FA,则可根据菱形的判定方法得到四边形ABDF是菱形;
(2)由于四边形ABDF是菱形,则AB∥DF,且AB=DF,再根据旋转的性质易得四边形ABCE为平行四边形,根据平行四边形的性质得AB∥CE,且AB=CE,所以CE∥FD,CE=FD,所以可判断四边形CDEF是平行四边形.
解答 (1)解:四边形ABDF是菱形.理由如下:
∵△ABD绕着边AD的中点旋转180°得到△DFA,
∴AB=DF,BD=FA,
∵AB=BD,
∴AB=BD=DF=FA,
∴四边形ABDF是菱形;
(2)证明:∵四边形ABDF是菱形,
∴AB∥DF,且AB=DF,
∵△ABC绕着边AC的中点旋转180°得到△CEA,
∴AB=CE,BC=EA,
∴四边形ABCE为平行四边形,
∴AB∥CE,且AB=CE,
∴CE∥FD,CE=FD,
∴四边形CDEF是平行四边形.
点评 本题考查了旋转的性质:旋转前后两图形全等;对应点到旋转中心的距离相等;对应点与旋转中心的连线段的夹角等于旋转角.也考查了平行四边形的判定和菱形的判定.

练习册系列答案
相关题目
1.长沙市中考体育分值已经提高到了60分,其中的必考项目就有男子引体向上和女子一分钟仰卧起坐,各校为此加强了对体育训练的重视.
引体向上(男)和一分钟仰卧起坐(女)共16分 单位:次数
注:0.5次是指考生从直臂悬垂开始,有正确的引体动作和下杠动作,但未完整完成一次
某中学对全校学生这两项运动的成绩进行了统计,规定分值15分及以上为优秀,12分到14分为良好,6分到10分为合格,6分以下不合格,在全校800名初三学生中,随机抽取部分学生进行测试,并将测试成绩绘制成如下两幅不完整的统计图,求:
(1)某女生说她得了12分,请问她一分钟做了多少次仰卧起坐;
(2)请问一共抽取了多少名学生?并补全条形统计图;
(3)根据抽样结果估计,本校项目由多少学生能够得优秀?

引体向上(男)和一分钟仰卧起坐(女)共16分 单位:次数
| 分值 | 16 | 15 | 14 | 13 | 12 | 10 | 8 | 6 | 3 | |
| 成绩 | 男(次) | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0.5 |
| 女(次) | 45 | 40 | 36 | 32 | 28 | 25 | 22 | 20 | <19 | |
某中学对全校学生这两项运动的成绩进行了统计,规定分值15分及以上为优秀,12分到14分为良好,6分到10分为合格,6分以下不合格,在全校800名初三学生中,随机抽取部分学生进行测试,并将测试成绩绘制成如下两幅不完整的统计图,求:
(1)某女生说她得了12分,请问她一分钟做了多少次仰卧起坐;
(2)请问一共抽取了多少名学生?并补全条形统计图;
(3)根据抽样结果估计,本校项目由多少学生能够得优秀?

2.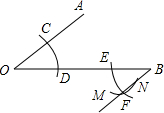 如图,用尺规作出了BF∥OA,作图痕迹中,弧MN是( )
如图,用尺规作出了BF∥OA,作图痕迹中,弧MN是( )
 如图,用尺规作出了BF∥OA,作图痕迹中,弧MN是( )
如图,用尺规作出了BF∥OA,作图痕迹中,弧MN是( )| A. | 以B为圆心,OD长为半径的弧 | B. | 以C为圆心,CD长为半径的弧 | ||
| C. | 以E为圆心,DC长为半径的弧 | D. | 以E为圆心,OD长为半径的弧 |
19.2015年10月上市的某品牌手机经过连续两次降价,截至2016年3月底售价由原来的6500元/台,降至4200元/台.设平均每个季度的降价率为x,根据题意,可列出方程是( )
| A. | 4200(1+x)2=6500 | B. | 4200(1+2x)=6500 | C. | 6500(1-x)2=4200 | D. | 6500(1-2x)=4200 |
1.已知二次函数y=ax2+bx+c(a>0)的图象经过点A(-1,2),B(2,5),顶点坐标为(m,n),则下列说法错误的是( )
| A. | c<3 | B. | m≤$\frac{1}{2}$ | C. | n≤2 | D. | b<1 |
 如图,在平行四边形ABCD中,过点B作BE⊥CD,垂足为E,连接AE,F为AE上一点,且∠BFE=∠C.
如图,在平行四边形ABCD中,过点B作BE⊥CD,垂足为E,连接AE,F为AE上一点,且∠BFE=∠C.
 如图,在△ABC中,AB=AC,∠BAC=50?.分别以B、C为圆心,BC长为半径画弧,设两弧交于点D,与AB、AC的延长线分别交于点E、F,连接AD.则
如图,在△ABC中,AB=AC,∠BAC=50?.分别以B、C为圆心,BC长为半径画弧,设两弧交于点D,与AB、AC的延长线分别交于点E、F,连接AD.则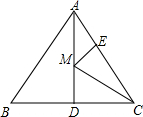 如图,等边△ABC的边长为6,AD是BC边上的中线,M是AD上的动点,E是AC边的中点,则EM+CM的最小值为3$\sqrt{3}$.
如图,等边△ABC的边长为6,AD是BC边上的中线,M是AD上的动点,E是AC边的中点,则EM+CM的最小值为3$\sqrt{3}$.