题目内容
8.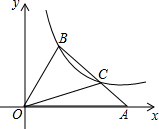 如图,在平面直角坐标系xOy中,△OAB的顶点A在x轴正半轴上,OC是△OAB的中线,点B,C在反比例函数y=$\frac{2}{x}$(x>0)的图象上,则△OAB的面积等于3.
如图,在平面直角坐标系xOy中,△OAB的顶点A在x轴正半轴上,OC是△OAB的中线,点B,C在反比例函数y=$\frac{2}{x}$(x>0)的图象上,则△OAB的面积等于3.
分析 过点B、点C作x轴的垂线,垂足为D,E,则BD∥CE,得出$\frac{CE}{BD}$=$\frac{AE}{AD}$=$\frac{AC}{AB}$=$\frac{1}{2}$,设CE=x,则BD=2x,根据反比例函数的解析式表示出OD=$\frac{1}{x}$,OE=$\frac{2}{x}$,OA=$\frac{3}{x}$,然后根据三角形面积公式求解即可.
解答 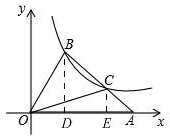 解:如图,过点B、点C作x轴的垂线,垂足为D,E,则BD∥CE,
解:如图,过点B、点C作x轴的垂线,垂足为D,E,则BD∥CE,
∴$\frac{CE}{BD}$=$\frac{AE}{AD}$=$\frac{AC}{AB}$,
∵OC是△OAB的中线,
∴$\frac{CE}{BD}$=$\frac{AE}{AD}$=$\frac{AC}{AB}$=$\frac{1}{2}$,
设CE=x,则BD=2x,
∴C的横坐标为$\frac{2}{x}$,B的横坐标为$\frac{1}{x}$,
∴OD=$\frac{1}{x}$,OE=$\frac{2}{x}$,
∴DE=OE-OD=$\frac{1}{x}$,
∴AE=DE=$\frac{1}{x}$,
∴OA=OE+AE=$\frac{3}{x}$,
∴S△OAB=$\frac{1}{2}$OA•BD=$\frac{1}{2}$×$\frac{3}{x}$×2x=3.
故答案为3.
点评 本题考查了反比例函数图象上点的坐标特征,反比例函数系数k的几何意义,平行线分线段成比例定理,求得BD,OA的长是解题关键.

练习册系列答案
 天天向上口算本系列答案
天天向上口算本系列答案
相关题目
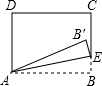 如图,在矩形ABCD中,AB=5,BC=3,点E为射线BC上一动点,将△ABE沿AE折叠,得到△AB′E.若B′恰好落在射线CD上,则BE的长为$\frac{5}{3}$或15.
如图,在矩形ABCD中,AB=5,BC=3,点E为射线BC上一动点,将△ABE沿AE折叠,得到△AB′E.若B′恰好落在射线CD上,则BE的长为$\frac{5}{3}$或15.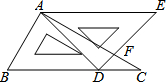 将一副学生用的三角板按如图所示的方式摆放,若AE∥BC,则∠AFD的度数是75°.
将一副学生用的三角板按如图所示的方式摆放,若AE∥BC,则∠AFD的度数是75°.